ビット計算

アルゴリズム（繰り返し計算）

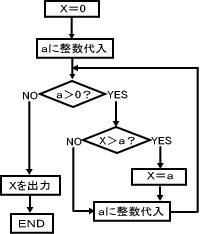
繰り返し計算のあるアルゴリズムは、プログラム構造わかりにくいという人が多いと思います。こういう人は、多少なりともなじみのある形（たとえばフロー図）に整理すると理解しやすくなります。
16年度の問題1-2-5を例にとって、フロー図による整理をやってみましょう。

================過去問題（Ｈ16問題1-2-5）================
ファイルから整数データ（最後のデータは０又は負数とする）を読み込んで計算を行なう、以下のプログラムについて、間違った記述を次の中から選べ。

・ｘの値を０とする
・ａに整数データを読み込む
・ａが正であれば以下のことを繰り返す
　　｛　・　ｘ＜ａならばｘにａの値を代入する
　　 　・　ａに整数データを読み込む
　　｝
・ｘの値を出力して終了する

(1) 読み込まれた正整数の中から最大値を選んでその値を出力する。
(2) ０又は負の整数が読み込まれると、計算結果を出力してプログラムは終了する。
(3) 最大値を選ぶ対象の整数は何個あってもよい。
(4) 最初に読み込まれる整数が負の場合、出力は行なわれない。
(5) ０又は負数の後に正整数があっても、読み込まれない。

プログラム部分をフローにします。右図を見てください。

●「〜する」というような、無条件に処理していく部分は、長方形の枠の中に実施内容を書いて、順に並べて矢印で実施手順を示す。
実施内容は、「Ｘの値を0とする」と、そのまま書いてもかまいませんが、「Ｘ＝0」というように式にできるものは式にしたほうが楽です。
●「〜ならば」といった、条件分岐は、ひし形の枠の中に判断基準を書き、YES/NO判断で左右に分かれるようにする。ここでも「ａが正」→「ａ＞0」というように式にします。
●繰り返し部分は、どこからどこまでが繰り返し処理内容かを読み取り（プログラムでは、インデントで字下げして、前後を「｛」「｝」などで囲って表示されることがよくある）、最後はどこへ戻るのかを把握する。
●処理終了部分には「ＥＮＤ」と明示する。なお、開始部分が見難い場合は、処理開始箇所に「ＳＴＡＲＴ」と明示するとわかりやすくなる。

これを見ながら、選択肢を検討していってみましょう。

(1) 読み込まれた正整数の中から最大値を選んでその値を出力する。
よくわかりませんね。実はこのアルゴリズムは最大値検索を目的としたルーチンなのですが、別にそんなことわからなくてもかまいません。明らかな間違いが見つかればそれでいいのですから、とりあえず正誤判断はせず、放っておきます。
(2) ０又は負の整数が読み込まれると、計算結果を出力してプログラムは終了する。
最初の条件分岐（ひし形部分）でａ＞0？に対してＮＯですから、「Ｘを出力」して「ＥＮＤ」に行きます。よって記述内容は正しいとわかります。
(3) 最大値を選ぶ対象の整数は何個あってもよい。
よくわからないので放っておきます。
(4) 最初に読み込まれる整数が負の場合、出力は行なわれない。
フローより明らかなように、「ａに整数代入」の後はａ＞0？の分岐に行きます。ここでａ＜0であれば「Ｘを出力」に行きます。よって、「出力は行われない」ことはありません。
ここで明らかな間違いが見つかったので、正解は(4)とし、検討を終了してもかまいません。
(5) ０又は負数の後に正整数があっても、読み込まれない。
最初の分岐でａ＞0でなければ「Ｘを出力」して「ＥＮＤ」に行き、プログラムは終了しますから、読み込み（ａに整数代入）はもう行われません。よって記述内容は正しいとわかります。
==========================================================

もう1問、過去問題を使って、フロー図化の練習をしてみましょう。

================過去問題（Ｈ13問題1-2-1）================
次に示すアルゴリズムを実行した結果、表示される値はいくらか。

アルゴリズムＥ
　・整数変数xの値を70とする；整数変数yの値を50とする；
　・xをyで割り算し、余りを整数変数rに代入する；
　・ｒ=0の条件が成立しない時は、以下の手順を繰り返す:(下の注を参照のこと)
　　　{・yをxに代入する；
　　　 ・rをyに代入する；
　　　 ・xをyで割り算し、余りを整数変数rに代入する；}
　・yの値を表示する；
注)まず、r=0の条件が成立するか調べ、成立しなければ{　}内の命令文を実行し、その後r=0の条件が成立するかどうかを調べる。成立しなければ{　}内の命令文を実行する。これを繰り返し、条件が成立したら繰り返しを終了して、次の表示命令文を実行する。

(1) 0
(2) 5
(3) 10
(4) 20
(5) 50

最初の2行は単純処理ですから、長方形枠を手順通りに並べます。処理内容は、「整数変数ｘの値を70とする」と、そのまま書いてもかまいませんが、「ｘ＝70」というように簡潔にしたほうがわかりやすくなります。2行目も「ｘ÷ｙ＝ｚ ．．．ｒ」というように式にします。
3行目は条件分岐です。「ｒ＝0」が条件で、YES（成立する）時は繰り返し部分（「｛」と「｝」で囲まれた部分）を飛ばして、その先にいきます。つまり「ｙの値を表示する」に行きます。「ｒ＝0」がNO（成立しない）場合は、繰り返しになります。
繰り返し内容は、単純処理が3つです。それぞれを式化し、長方形枠に書きます。
「ｙをｘに代入する」→「ｘ＝ｙ」
「ｒをｙに代入する」→「ｙ＝ｒ」
「ｘをｙで割り算し、余りを整数変数ｒに代入する」
　　　　　　　　　　　　　　　　　　→「ｘ÷ｙ＝ｚ　余りｒ」
その後、繰り返しの頭部分、すなわち条件分岐のところに戻ります。これをみると、ｒ＝0かどうかの判断をして、ｒ≠0であれば、繰り返し内の処理（3ステップ）を行い、またｒ＝0かどうかの判断をして、ｒ≠0であれば････というような繰り返し処理であることが理解できます。
==========================================================

なお、H13問題は値（最後に表示されるｙの値）を聞いています。処理内容の正誤を聞くH16問題とは、問う内容が異なります。
値を聞いてくる問題で、かつ、フロー化しなくてもプログラム手順通りの実行ができる（トライアル計算できる）場合は、トライアルしてしまったほうが速くなります。
この視点で過去問題を見ると、
　　　H13････値を聞くので、トライアルのほうが速い
　　　H14････処理内容を理解しないと答えられないので、フローを作成
　　　H15････2問とも、処理内容を理解しないと答えられないので、フローを作成
　　　H16････処理内容を理解しないと答えられないので、フローを作成
となり、フローを書いたほうがいい問題例が圧倒的に多くなっています。

最後に練習問題をやってみましょう。

構文図

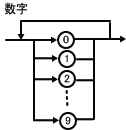
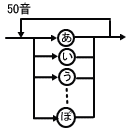
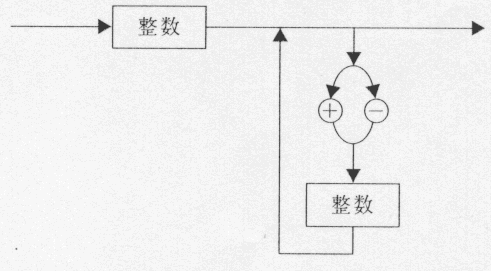
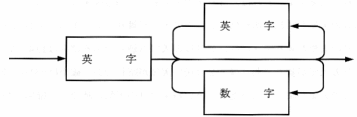
構文図は、文法を図化したもので、厳密な、あいまいさのない文法が必要な世界、つまりプログラミングの世界でよく使われます。

最も単純な構文図を右図に示します。
文章（文字列）を左から流すと、1文字ずつ流れていきます。枝分かれして、数字の0〜9のどれかと合致すると、その先に行きます。文字列が終わっていれば（文章を構成する文字が全部通過したら）終了、そうでなければ戻って、次の文字を枝分かれに流します。
もし文字列の中に条件に合致しない文字、（右の例だと数字以外の文字）が入っている場合、通過できずにエラーとなります。逆に言うと、この構文図に合致する文字列は、数字のみから構成される文字列、つまり「数字」だということになります。

図−１	図−２	図−３	図−４

構文図の説明が見られるサイトはいくつかありますので、そちらをよく読んで理解してください。

それでは、構文図が出題された過去問題を見てみましょう。

==============過去問題（平成16年度）==============
構文図を用いて文字列の集合を定義することができる。例えば、図1の構文図は整数の加減算式を定義している。この定義に従えば、1＋2−3や1−2が整数の加減算式であることがわかるが、+1や-1は加減算式ではない。
　

次の文字列のうち、図2の構文図では定義されていないものを選べ。

(1)　ａ
(2)　ｂ
(3)　ａｂ
(4)　ｂａ
(5)　ａａａ

図1およびその説明は、構文図の説明なので問題には無関係です。
図2を見ると、最初の「関所」は、「ａ」以外ならそのまま通過し、「ａ」ならフリーパスか、あるいはループで戻るというものです。「ａ」が続く限りループできますから「ａａａａ」もＯＫですね。
2番目の「関所」は「ａ」か「ｂ」以外は通してくれませんから、どちらか以外の文字列を含んでいると通過できません。
選択肢(1)や(2)は第1関門をフリーパスし、第2関門でそれぞれ［ａ」と「ｂ」を通って終了というものです。
また(3)は第1関門の1回目で「ａ」のループを通り、第1関門の2回目はフリーパス、第2関門の「ｂ」を通っています。
(5)は第1関門の「ａ」ループを2回通った後、第2関門の「ａ」を通ったものです。
ところで第2関門の後はループがありませんから、この「ａ」や「ｂ」が文末文字ということになります。「ａ」は第1関門のループでも出てきますから、「ａ」の後に文字列が続くことはありえますが、「ｂ」の後に文字列が続くことはありえません。
よって、(4)がありえないということになります。
==================================================
==============過去問題（平成16年度）==============
あるプログラミング言語で使われる名前（変数名や関数名）は、次の構文図で規定されているものとする。この時、名前でないものを選べ。ただし、英字はa，b，･･･，z、A，B，･･･，Zのどれか、数字は0，1，･･･，9のどれかである。


(1) A　　　(2) name　　　(3) B740　　　(4) C6H6　　　(5) 11PM

「英字」「数字」とも非終端記号ですから、別途定義されており、その内容は問題文に「ただし」の後に記載されています。
第1関門が「英字」であり、それ以外の道はありませんから、1文字目が英字でない文字列は通過できません。つまり、(5)が正解になります。
==================================================

２進数

２進数とは
Ｎ進数とは、ゼロから数値を増やしていって、Ｎになったら桁を１つ上げて、元の桁はゼロにリセットするというものです。
私達が普通使っているのは10進数ですね。0、1、2、3････と増やしていって、10になったら、２桁目（10の位）の数値を１つ増やして、１桁目はゼロに戻します。つまり、「10」になります。
では２進数はどうなるでしょう。0、1、ときて、2になったら、２桁目を１つ増やして、１桁目はゼロにします。つまり、
　0、1、2
ではなく、
　0、1、10
となります。
さらに増やしていくと、10の次は１桁目がゼロから1つ増えて1になり、11となります。その次は、１桁目が2になるので、再び２桁目を１つ増やして１桁目はゼロに戻します。
ところがこのようにすると、２桁目が１から１つ増えて２になってしまいます。そこで今度は３桁目を１つ増やして２桁目はゼロに戻します。つまり、
　　11+1＝12
　→１桁目の2を0にして２桁目を1つ増やす→20
　→２桁目の2を0にして３桁目を1つ増やす→100
となります。このようにして、２進数の数値と１０進数の数値を比べてみましょう。

２進数では、１０進数の2、4、8、16で桁が上がっていますね。これらはそれぞれ2¹、2²、2³、2⁴に相当しますね。１０進数でも桁が上がるのは10、100、1000、10000で、それぞれが10¹、10²、10³、10⁴に相当しますから、この点は同じです。つまり、Ｎ進数ではＮ¹、Ｎ²、Ｎ³、Ｎ⁴････で桁が上がるのです。

２進数〜１０進数変換
１０進数の数値を２進数に変換するには、次のようにすればできます。
例として、１０進数の13を２進数に変換してみます。

(1)	13÷2＝	6　あまり　1	↑	あまりを下から上に逆順に読んで並べる
(2)	6÷2＝	3　あまり　0	↑
(3)	3÷2＝	1　あまり　1	↑
(4)	1÷2＝	0　あまり　1	↑

このように、商がゼロになるまで2（Ｎ進数のＮ）で割って、あまりを(4)→(1)の順に（計算して出てきたとは逆順に）並べます。こうすると「1101」が得られます。これが１０進数の13を２進数に変換した答えです。
今度は２進数を１０進数に変換します。 これは、Σ（2^桁数Ｎ-1×Ｎ桁目の数値）とすればＯＫです。
２進数の1101を１０進数に変換してみましょう。
　　４桁目→2^(4-1)＝2³＝8で、ここが1なので8×1＝8
　　３桁目→2^(3-1)＝2²＝4で、ここが1なので4×1＝4
　　２桁目→2^(2-1)＝2¹＝2で、ここが0なので2×0＝0
　　１桁目→2^(1-1)＝2⁰＝1で、ここが1なので1×1＝1
　　合計して、8+4+0+1＝13

２進数は何に使うか
コンピュータは電子機器ですから、回路に電流が流れているか流れていないかの２つに１つです。流れている状態（ＯＮ）を１、流れていない状態（ＯＦＦ）を０とすれば、この組合せで情報が伝達できます。
４つの回路のＯＮ/ＯＦＦの組み合わせで情報を送ると、
　　0000、0001、0010、0011、0100、0101、0110、0111、1000、1001、1010、1011、1100、1101、1110、1111
の１６通りの情報が流せます。前表のように、これは１０進数で10〜15にあたります。コンピュータでは、この１６通りの情報を１６進数で扱います。

論理演算

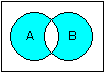
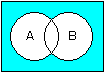
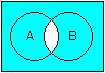
論理演算とは、真か偽かの2通りの結果だけを使った、集合における演算で、プログラミング言語などではビット演算とも言います。
与えられた命題が正しい場合を真（true）、正しくない場合を偽(false）といいます。
ここで「命題」とは、論理学用語で、意味に不明瞭なところがない文章のことです。
たとえば「私の身長は170cm以上である」という文書は、あいまいな点がないので命題です。一方、「私は忙しい」というのは、「忙しい」のところにあいまいさ・不明瞭さがある（「忙しい」と「忙しくない」の間の明瞭な境界がない）ので、命題とはいいません。
さて、「私の身長は170cm以上である」という命題に対し、身長175cmの人を当てはめると、命題は正しくなります。よって、真です。
身長165cmの人を当てはめると、命題は正しくなくなります。よって、偽です。
このように、同じ命題でも、当てはめる要素によって真偽は異なることがあります。

論理演算には、以下のものがあります。
ORとNOR、ANDとNANDは、それぞれの否定なのでわかりやすいと思います。ちょっとややこしいのはXORです。XOR＝OR-ANDと理解してください。
試験で必要になることが考えられる知識は、上の3つ程度と思われます。

演算種類	演算結果が真となる条件	イメージ（ベン図）
論理和 ＯＲ	ＡとＢのいずれかが真である（両方真でもＯＫ）
論理積 ＡＮＤ	ＡとＢのいずれもが真である
排他的 論理和 ＸＯＲ	ＡとＢのいずれか一方のみが真である
論理和 の否定 ＮＯＲ	ＯＲの真偽反転（ＯＲで偽であるものが真となる）
論理積分 の否定 ＮＡＮＤ	ＡＮＤの真偽反転（ＡＮＤで偽であるものが真となる）
論理否定 ＮＯＴ	真偽反転（真であれば偽に、偽であれば真になる）

たとえば、命題Ａが身長170cm以上、命題Ｂが体重60kg以上としてみます。これに対して、様々な身長・体重の場合に、論理演算の結果がどうなるかみてみます。なお、下表の中で○は真、×は偽です。