練習問題の答え
【基礎科目練習問題:システムの信頼性】 正解:3
並列システムの信頼性は、1−(1−システムAの信頼性)*(1−システムBの信頼性)。
たとえば信頼性90%のシステムを2つ並列に組み合わせると、その信頼性は、1-(1-0.90)*(1-0.90)=1-0.1*0.1=1.-0.01=0.99=99%となる。
問題では、88%のシステムと何かを並列にして99%なので、1-(1-0.88)*(1-x)=0.99。よってx=1-(1-0.99)÷(1-0.88)=0.917。
よって、正解は92%。(1-(1-0.88)*(1-0.92)=0.9904>0.99)
【基礎科目練習問題:待ち行列】 正解:2
解答選択肢の単位が分なので、単位時間を1分とする。
受付処理時間が10秒なので、1分あたり処理人数は、60秒/10秒=6人 よって、μ=6
来館者が1時間あたり300人なので、1分あたり来館者数は、300人/60分=5人 よって、λ=5
所要時間=1/(μ−λ)=1/(6−5)=1/1=1。
平均所用時間は1分。よって正解は(2)。
【基礎科目練習問題:コスト最小化】 正解:2
トータルコストなので、コストV=500X+4500/(1+X)。
数字が大きいので計算を楽にするため、コストの単位を百万円にすると、V(百万円)=5X+45/(1+X)。
解1:微分を使う
(1) トータルコスト計算式を整形する。
C=5X+45/(1+X)={5X(X+1)+45}/(X+1)=(5X2+5X+45)/(X+1)
(2) y=f(x)/g(x)に当てはめる。
f(x)=5X2+5X+45、g(x)=X+1とおきます。
(3) 微分する。
f(x)=5X2+5X+45より、f’(x)=10X+5
g(x)=X+1より、g’(x)=1ですから、
dx/dy={f(x)g’(x)−f’(x)g(x)}/g(x)2={(5X2+5X+45)*1−(10X+5)*(X+1)}/(X+1)2=0
(4) 整形して因数分解し、Xを求める。
dx/dy=0なので、分母がどれだけであろうと分子が0。よって、
(5X2+5X+45)*1−(10X+5)*(X+1)=0
=5X2−10X2+5X−10X−5X+45−5=−5X2−10X+40=0
左辺を−5で除して、X2+2X−8=0
これを因数分解すると、(X+4)(X-2)=0より、X=2,−4が求められる。X>0だから、X=2。よって正解は(2)。
として解いていくが、計算式がパッと出てこなければ簡単な計算なのでトライアルしたほうが早い。
トライアルすると下表のようになる。
| 強度X |
コストV |
| 1 |
27.50 |
| 2 |
25.00 |
| 3 |
26.25 |
| 4 |
29.00 |
| 5 |
32.50 |
【基礎科目練習問題:ビット計算】 正解:3
10進数の13を2進数に変換し、各桁の数値が各ビットに割り当てられた許可の可・不可に対応する。
10進数の2進数変換は、次のようにするとわかりやすい。
10進数の8を2進数に変換してみる。
8÷2=4 余り 0
4÷2=2 余り 0
2÷2=1 余り 0
1÷2=0 余り 1
というように、2で割っていって、商が0になった時点で終了する。そして、各計算ステップでの余りを右から順に並べる。これが10進数を2進数変換した結果であり、10進数の8は2進数で1000である。
次に問題の10進数の13を2進数に変換してみる。
13÷2=6 余り 1
6÷2=3 余り 0
3÷2=1 余り 1
1÷2=0 余り 1
となり、余りを右から並べると1101になる。つまり10進数の13は2進数の1101である。右から読取、作成、更新、消去に割り当てられているから、その可否は下表のとおりとなる。よって、作成以外は可能であり、正解選択肢は(3)となる。
| 消去 |
更新 |
作成 |
読取 |
| 1 |
1 |
0 |
1 |
| ○ |
○ |
× |
○ |
【基礎科目練習問題:アルゴリズム】 正解:2
処理内容をフローにしてみる(右図)。
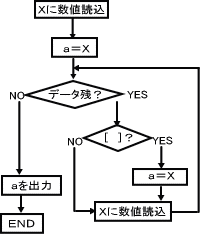
最初の2行は単純処理。数値データをVとすれば、1行目は「x=V」、2行目はa=x。
3行目は条件分岐。「数値データが残っていれば」なので、ひし形枠に「数値データ残」とでも書く。
YESなら繰り返し、NOなら繰り返しを飛ばして次の処理、つまり、「aを出力」→「END」へ。
繰り返し内容を見ると、[ ]内は条件分岐の判断基準とわかる。
ここでYESなら「aにxの値を代入」→「a=x」の処理。その後、YESでもNOでも「x=V」処理をして繰り返し。
フローを見ると、繰り返し内は、条件[ ]が成立した場合にのみ「a=x」処理を実行し、データのある限り繰り返し処理を行うというルーチンであることがわかる。
ここで、このプログラムの目的は最小値の抽出であることから、最後に出力されるaが最小値であることがわかる。また、xは、「数値データから値を読み込む」ことから、繰り返し処理の度に、数値データ群から読み込まれる値であることがわかる。つまり、繰り返し内の「a=x」処理は、「最小値の入れ物」である変数aに、数値データ群から読み込んだ値であるxを代入する処理であることがわかる。
さて、aには、繰り返し開始前に(2行目で)、数値データ群の最初のデータ(1行目でxに読み込んだ値)を代入してある。したがって、1回目の繰り返し処理内で、「a=x」をやってもやらなくても、aの値は変わらない。しかしこの後、xに数値データから値を読み込むので、xには数値データ群の2番目のデータが入る。つまり、2回目の繰り返し処理時点では、aに入っているのは数値データ群の最初の値、xには同じく2番目の値が入っている。よって、もし「a=x」を行うとすると、aが「最小値の入れ物」であることから、xがその時点での最小値である、すなわち「それまでの最小値」であるaより小さい値であるということが、「a=x」処理を行う条件であることがわかる。
以上より、「xがaより小さい」ということは「aがxより大きい」とうことであるから、正解は(2)である。
