並列化によるシステムの信頼性評価

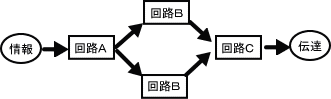
たとえば、ある情報が回路Ａ→回路Ｂ→回路Ｃを経て伝達されるとします。それぞれの回路が正常に動作すれば正常な情報伝達ができますが、たまに異常動作をして伝達できないこともあります。この正常動作する確率が信頼性です。

今、回路Ａの信頼性が90％としましょう。つまり、100回の情報伝達をするとき、1回は伝達不良を起こしてしまうということになります。回路Ｂ、回路Ｃも信頼性が90％であったとすると、全体の信頼性はどうなるでしょう。
上図のような配列を直列といいますが、直列のときの信頼性は、それぞれの信頼性をかけあわせたものになります。すなわち、90％×90％×90％＝0.9×0.9×0.9＝0.729≒73％となります。

ここで、回路Ｂを２回線設けて、回路Ｂが駄目な場合は回路Ｂ’を通って伝達するようにしてみます。

このような配列を並列といいます。この部分の信頼性は、回路Ｂも回路Ｂ’も同時に不良動作を起こさない限り、情報は伝達できるのですから、それぞれの不良動作確率（1-信頼性）をかけあわせ、それを1から引いたものになります。つまり、1-（1-0.9）×（1-0.9）＝0.99＝99％となります。並列は、並べれば並べるほど信頼性はアップします。
全体の信頼性について見てみましょう。回路Ｂの部分の信頼性が並列化により99％になりましたから、90％×99％×90％＝0.9×0.99×0.9＝0.802≒80％となり、全体の信頼性もアップしています。
つまり、こういうことです。

●直列システムの稼働率＝システムａの稼働率×システムｂの稼働率
●並列システムの稼働率＝１−（１−システムａの稼働率）×（１−システムｂの稼働率）
●直列より並列のほうが信頼性が高い
このように、システムの信頼性をアップするための方法の１つとして、同一機能を有するユニットを複数設けるというものがあります。これを冗長化といい、直列型システムを並列型システムにすることで信頼性を向上させることを並列冗長化といいます。

以上を踏まえて過去問題を見てみましょう。

==============過去問題（平成13年度）==============
次の図に示されるシステムの設計を考える。各システムは、節点を連結する線要素から構成されており、節点から節点に進むことのできる可能性(要素の信頼性)は90%である。ここで、それぞれのシステムを用いて左端から右端の節点に進むことのできる可能性、すなわち、システム全体の信頼性が最も高いのはどれか。　

(1)　A
(2)　B
(3)　C
(4)　D
(5)　E

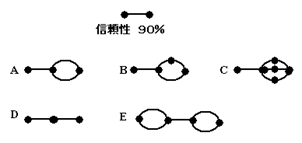
Ｄは直列だけなので、並列を含むシステムより信頼性が低いことは明らかです。
次にＥを見てみると、Ａの前に並列が1つ加わった形になっています。いくら信頼性の高い並列とはいえ、1よりは小さい（異常の起こる可能性がゼロではない）のですから、わずかでもＡより信頼性は低くなります。
よって、答えはＡ〜Ｃに絞られます。
ＡとＢを比べると、Ｂは並列の1ルート内に直列が1つ加わっています。ですからその分だけＡより信頼性は低くなります。
よって、答えはＡとＣに絞られました。
ここで、Ａで並列になっている部分だけに着目して計算します。
（Ａ）90％の並列なので、1-（1-0.9）*（1-0.9）＝0.99
（Ｃ）90％の直列が3つ並列になっている。まず直列部分の信頼性は、0.9*0.9＝0.81。これが3つ並列なので、1-（1-0.81）*（1-0.81）*（1-0.81）＝0.993。
よってＣのほうが信頼性が高い。答えは選択肢(3)。なお、0.81を0.8とすれば、暗算でもＣ＞Ａと判断できる程度の計算はできます。
この問題のポイントは、以下の２つです。
　(1) 図からシステム信頼性・直列並列の知識で解けばいいということを見つけること
　(2) 横棒が直列、メガネ形が並列を表すこと
これが分かれば楽勝、分からなければギブアップです。
また、問題を効率よく解く上でのポイントは、選択肢を比較するということです。各選択肢の信頼性を計算してから比較するのではなく、たとえばAとDの違いは２つ目の節点間が直列か並列化の違いだけである点に注目するなど、「どこが違うか」に視点を置いて比較することができれば、計算などほとんど不要です。
===============================================

==============過去問題（平成16年度）==============
図に示される左端から右端に情報を伝達するシステムの設計を考える。図中の数値は、構成する各要素の信頼度を示す。また、要素が並列につながっている部分は、少なくともどちらか一方が正常であれば、その部分は正常に作動する。
システムＢのシステム全体の信頼度を、システムＡのシステム全体の信頼度と同じにするためには、システムＢの各要素の信頼度Ｘをいくらにすれば良いか。次のうち最も近いものを選べ。なお、システムＢを構成する各要素の信頼度は同じであるとする。

システムA
システムB

(1) 0.87　　　(2) 0.90　　　(3) 0.93　　　(4) 0.96　　　(5) 0.99

システムＡの信頼性は、並列部が1-（1-0.9）*（1-0.9）＝0.99で、これと0.92つの直列ですから、0.9*0.99*0.9＝0.80となります。
システムＢは信頼性Ｘが3つ直列なので、Ｘ*Ｘ*Ｘ＝Ｘ³＝0.80となります。つまり、Ｘ＝0.80^1/3なのです。三乗根の出せる電卓があれば、0.80^1/3＝0.93とすぐ出ますので、正解は選択肢(3)とわかります。
電卓がなければ、次のようにすれば暗算でも解けます。
システムＡ、Ｂを比較すると、並列が入っている分だけシステムＡのほうが信頼性が高いものになっています。にもかかわらず全体の信頼性が同じということは、システムＢは個々の信頼性がシステムＡより高いということです。これで選択肢(1)と(2)は消えます。
システムＡの信頼性は、0.9*0.99*0.9ですが、0.9*0.9＝0.81なので、「0.81*0.99でだいたい0.8」と暗算できます。
よって、システムＢの信頼性はＸ³＝0.80で、Ｘ＝0.80^1/3です。
【方法１：トアイアル計算する】
ここで残った選択肢(3)〜（5）の真ん中あたりの0.95で試算します（0.96でもいいのですが、暗算しやすい0.95にします）。
Ａ×0.95ということは、Ａ-Ａ×0.05ということです。0.95×0.95＝0.95-0.95×0.05≒0.95-0.048くらいなので、0.9くらい。
0.9-0.9×0.05＝0.9-0.045＝0.855くらい。これではシステムＡの0.8より高すぎます。
よって答えは0.90より大きく、0.95より小さい選択肢で、これは(3)しかありません。
【方法２：電卓を使う】
ここでは、持込可能なメモリ・関数機能のない電卓（１００円ショップの電卓と同じような電卓）を使って解いてみます。
電卓は、数値を入力したあとに√（ルート記号）を押せば、平方根、すなわち1/2乗の答えが出ます。ここでもう一度ルートを押すと、ルートのルート、すわなち1/2乗×1/2乗＝1/4乗が出ます。ちなみにもう一度ルートを押すと、1/16乗が出ます。0.80^1/3ということは、0.80^1/2と0.80^1/4の間になります。そして0.80を入力したあとルートを１回押せば0.80^1/2が、さらにもう１回押せば0.80^1/4が得られます。やってみると、0.80^1/2＝0.894、0.80^1/4＝0.946で、はこれらの間にあることがわかります。この条件にある選択肢は(2)と(3)しかありません。0.80^1/2＝0.894と0.80^1/4＝0.946を平均すると0.92で、(3)に近いので(3)が答えです。
H13の問題に比べれば、最初から並列とかシステム信頼度などと書いてあり、図も直列並列がわかりやすく書かれているので、この問題をシステム信頼性の知識で解くことはすぐわかると思います。もしわからなければ、最初から勉強していないということなので、これは論外です。
システムＡの信頼性は、直列・並列の式さえ知っていればできますから、これも簡単です。あとは、システムBの信頼性がＸ³であると分かればいいのですが、これも直列の式さえ知っていればできるはずです。
問題は、Ｘ＝0.80^1/3とわかってから、三乗根をどうやって算出するかではないかと思います。この問題はトライアル計算でも十分対応できますが、できれば電卓を使えたほうが効率的です。
===============================================

==============過去問題（平成17年度）==============
下図は、システム信頼性解析の一つであるFTA(Fault Tree Analysis)図である。図で、記号(ａ)は、その下流(下側)の事象が同時に生じた場合に、上流(上側)の事象が発現することを、記号(ｂ)は、下流の事象のいずれかが起きた場合に上流の事象が発現することを意味する。事象Ａが発現する確率に最も近い値を選べ。最下段の枠内の数値は、最も下で起きる事象の発現確率を表す。なお、記号の下流側の事象の発生はそれぞれ独立事象とする。


(1) 　0.200　　(2) 　0.044　　(3) 　0.048　　(4) 　0.203　　(5) 　0.204

（１段目）左下：0.1 OR 0.1→1-（1-0.1）*（1-0.1）＝1-0.9*0.9＝1-0.81＝0.19
　　　　　その右：0.2 AND 0.2→0.2*0.2＝0.04
（２段目）上記より0.19 OR 0.04→1-（1-0.19）*（1-0.04）＝1-0.81*0.96＝0.2224
（３段目）上記より0.222 AND 0.2→0.222*0.2＝0.0444
よって正解は(2)。
フォールトツリーという実務技術が出てきましたが、何をやっているのかさえわかれば、簡単な問題です。
ＡＮＤとＯＲの解説が書いてありますが、システム信頼性のＡＮＤは直列を、ＯＲは並列を表すことがわかっていれば問題ありません。●ＡＮＤ■は●×■、ＯＲは1-（1-●）×（1-■）です。
===============================================

==============過去問題（平成17年度）==============
単位期間中の故障発生確率が１％であるように調整されたシステムがある。このシステムを100単位期間稼動させたとき、この期間内に故障がまったく発生しない確率は次のうちどれに最も近いか。ただし個々の単位期間における故障の発生は、それぞれ独立事象とする。

(1) ほぼＯ　　　(2) 約１／３　　　(3) 約１／２　　　(4) 約２／３　　　(5) ほぼ１

故障発生確率が1％ということは、故障が発生しない確率は99％。
これが100回繰り返して成立する確率なので、0.99の直列（AND条件）。
よって、0.99¹⁰⁰＝0.366≒1/3。（あるいは（1-0.01）100＝0.366≒1/3でもよい）
よって、正解は2。
●AND条件（直列）は掛け合わせる････A AND B　→　A*B
●OR条件（並列）は1から除したものを掛け合わせて最後に１から除する････A OR B　→　1-（1-A)*（1-B)
ということを覚えていて、応用できるかどうかの勝負です。
なお、0.99¹⁰⁰という計算は、１００円電卓でも比較的簡単にできます。
【独立事象】
この問題では、独立事象についてもよく理解しておく必要があります。そうでないと、
　「1％×100＝100％なので(1)」
とか、
　「100回に1回壊れる。100単位時間だから100回なので、1回は壊れる。だから(1)」
といった間違いをしてしまいます。
たとえば、
　「100枚のカードの中に1枚だけジョーカーが入っている。1枚カードを引くことを100回繰り返して、一度もジョーカーに当たらない確率は？」
という問題があるとします。
カードを引くたびに残りカードが減るのであれば、ロシアンルーレットになりますから、いつかはジョーカーを引きます。ですから一度も引かない確率はゼロです。でも、これは独立事象ではありません。なぜなら、カードを戻さないということは、2回目にはジョーカーを引く確率は1/100ではなく、1/99になっているからです。つまり、1回目の結果が2回目に影響を与えているからです。
独立事象であれば、カードを1回ひくたびに元に戻して100枚にして、シャッフルして、再度引くことになります。つまり、1回ごとにリセットします。
現実には独立事象というのは、そうそうあるものではありません。故障率1/100のシステムにしても、たとえばこれが機械なら、稼働時間が長引けば油が切れたりいろいろして故障率がアップしてきます。でも、独立事象と断ってありますから、たとえば1時間稼動するたびにオーバーホールして故障率を1％に調整して、また1時間稼動して････という繰り返しをしているような状況になります。
===============================================

最後に練習問題をやってみましょう。

オペレーションズリサーチ（待ち行列）

サービス窓口における「順番待ち」を数式化したものです。
重要な要素に、到着分布（列に到着する客の数と時間の関係）やサービス分布（サービスの数と時間の関係）がありますが、出題される場合は、単純化するため、到着分布はポアソン分布に従い、サービスに要する時間は指数分布に従うものとするはずです。すなわち、まとまって到着したり、数を溜めてからいっせいにサービスしたりするのではなく、到着もサービスも、だらだらと一定の調子で行われるということです。
こういった条件で成立する、もっとも単純な待ち行列数学モデルは、次のようなものです。
　単位時間当たりの到着数：λ
　単位時間当たりサービス処理数：μ
　ρ＝λ/μ
とした場合、
●システム内にｎ人の客がいる確率
　　Ｐｎ＝ρ^ｎ（１−ρ）
●客が待たずにサービスを受けられる確率
　　Ｐ_empty＝１−ρ
●客が待たなければならない確率
　　Ｐ_full＝ρ
●システム中にいる平均客数
　　Ｌ＝ρ/(１−ρ)＝λ/(μ−λ)
●待っている客数の平均値
　　Ｌｑ＝ρ²/(１−ρ)
●客がシステム中に滞在する平均時間
　　Ｗ＝1/(μ−λ)
●客がシステムに到着してからサービスを受けられるまでの平均待ち時間
　　Ｗｑ＝λ/{μ(μ−λ)}
といったような数式が成り立ちます。
なお、実際の試験では、数式があらかじめ示されると思われますので、上式を覚える必要はないと思います。与えられた式で素直に代入し計算すればいいと考えましょう。

以上を踏まえて過去問題を見てみましょう。

==============過去問題（平成14年度）==============
あるコンビニエンスストアには、12：00〜13：00の間に90人の客が来店する。この店にはレジ１台が設置されており、会計処理に要する時間は客１人当たり平均0.5分である。このとき、客がレジに並んでから会計が終了するまでの平均の時間は何分か、次のうちから答えよ。ここでは、単位時間当たりに客が訪れる数の分布はポアソン分布に従い、会計処理に要する時間は指数分布に従うものとする。なお、本問題に関係した公式を次に示す。
　　　　　　　　平均応対時間（待ち時間＋処理時間）＝1/（1-ρ）・1/μ
ここで、μ：単位時間当たりの平均処理人数、ρ：処理率（＝λ/μ）、λ：単位時間当たりの平均到着者数である。

(1)　0.5（分）
(2)　1.0（分）
(3)　2.0（分）
(4)　3.0（分）
(5)　5.0（分）

平均対応時間Ｗ＝1/（1-ρ）・1/μとしていますが、ρ＝λ/μを代入すれば教科書通りのＷ＝1/(μ−λ)となります。
求められる答えの時間単位が「分」なので、単位時間を1分とします。
単位時間当たり平均到着数λ＝90人/時＝1.5人/分
単位時間当たり平均処理人数μ＝1人/0.5分＝2人/分
よって、対応時間Ｗ＝1/(μ−λ)＝1/(2−1.5)＝1/0.5＝2分
問題文に示された式をそのまま使う場合、処理率ρ＝λ/μ＝1.5/2＝0.75
平均応対時間＝1/（1-ρ）・1/μ＝1/（1-0.75）*1/2＝1/0.25*1/2＝4*1/2＝2分
===========================================

最後に練習問題をやってみましょう。

最適化（線形計画〜コスト最小化）

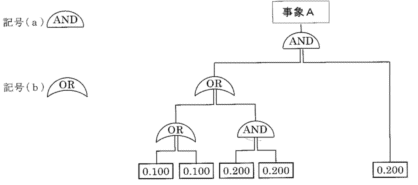
13・14・15年度と、３年続けて出題されたのが、コスト最小化の問題です。何らかの損害を防ぐために、相応のコストがかかります。ここにおいて、コストと見込み損害額（主に発生時の損害額×発生確率）を足したトータルコストを最小にするようなＸを求めよ、というものです。

最後に練習問題をやってみましょう。

最適化（線形計画・図解法〜利益最大化）

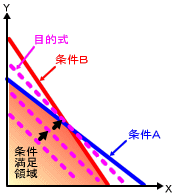
たとえば工業立地について考えてみます。用地や工業用水に供給可能な限界がある中で、誘致可能な工業の種類がいくつかあるとします。このような場合において、最大の生産額をあげるためには、どの工業をどれだけ誘致すればいいでしょうか。
このことを考察するための条件式として、
　Σ（各工業が必要とする供給物の量×各工業の誘致量）≦供給物の限界（条件）
　各工業の誘致量≧0
があります。また、目的式は、
　生産額＝Σ（各工業の生産額×各工業の誘致量）
となります。このように、制約条件式、目的式とも一次式で表すことのできる場合、この方法を線形計画法といいます。
扱う要素（工業、供給物）の種類が2つであれば、図解法によって最適解を導くことができます。
次のような例を考えてみます。

用地の制限は240ha、用水の制限は100t/日であり、それに対して工業Aは用地40ha、用水25t/日を、工業Bは用地50ha、用水15t/日を必要とします。また生産額は、工業Aが30百万円、工業Bが25百万円です。
工業Ａ、工業Ｂの誘致量（立地単位数）をそれぞれＸ、Ｙとすれば、条件式は、
　（条件Ａ）40Ｘ＋50Ｙ≦240
　（条件Ｂ）25Ｘ＋15Ｙ＝100
　（条件Ｃ）Ｘ≧0、Ｙ≧0
また目的式は、総生産額をＰとすれば、
　Ｐ＝30Ｘ＋25Ｙ
となります。
わかりやすく、条件式と目的式をＹ＝ａＸ＋ｂの形にしてみましょう。
　（条件Ａ）　40Ｘ＋50Ｙ≦240　→　Ｙ≦−40/50Ｘ＋240/50＝−0.8Ｘ＋4.8
　（条件Ｂ）　25Ｘ＋15Ｙ≦100　→　Ｙ≦−25/15Ｘ＋100/15＝−1.67Ｘ＋6.67
　（目的式）　30Ｘ＋25Ｙ＝Ｐ　　→　Ｐ＝−30/25Ｘ＋Ｐ/25＝−1.2Ｘ＋Ｐ/25
条件式をグラフにすると、右図のようになります。条件Ａと条件Ｂによって制限された領域が、用地・用水の制限上限を満足する領域です。
目的式は破線で示した傾きを持つ直線で、様々な値を取りますが、原点から離れるほど（図中黒矢印の方向に行くほど）生産額Ｐが大きくなっていきます。しかし条件満足領域から外れてはいけません。
よって、条件を満足しつつ最大の生産額となるのは、条件Ａと条件Ｂのグラフ交点を通るときであることが、図から読み取れます。
これは、目的式の傾きが条件Ａと条件Ｂの中間にあるためで、もし目的式の傾きが条件Ｂより急であれば、条件ＢグラフとＸ軸の交点（すなわち、Ｙ＝0より、工業Ｂの誘致数は0で工業Ａのみ誘致）が、また逆に目的式の傾きが条件Ａより緩やかであれば、条件ＡとＹ軸の交点（Ｘ＝0より、工業Ｂのみ誘致）が、それぞれ最大生産額を見込める条件となります。
さて、図のような場合、条件Ａと条件Ｂの交点は、連立方程式を解けば求められます。
　（条件Ａ）Ｙ≦−0.8Ｘ＋4.8
　（条件Ｂ）Ｙ≦−1.67Ｘ＋6.67
よって、条件Ａ−条件Ｂとして0≦0.87Ｘ−1.87、よってＸ≧1.87/0.87＝2.15となり、Ｙ≦−0.8Ｘ＋4.8＝−0.8*2.15＋4.8＝3.08となります。
よって生産額は、Ｐ＝30Ｘ＋25Ｙ＝30*2.15＋25*3.08＝142百万円となります。
以上、図解法について解説しましたが、図を描かなくても、条件式・目的式をＹ＝ａＸ＋ｂの形で式化すれば、条件Ａ・Ｂの交点あるいは条件式とＸＹ軸の交点でＸ、Ｙを求めることができます。
なお、要素が3つ以上になると図解法では無理で、シンプレックス法などを用いねばならなくなりますが、これは複雑なので出題される可能性は低いと思われます。