次の問題に答えよ。

１．ψ= f ( x , y , z ) = 3 x³−x²yz+ xy²z²+yz³のとき、ψをxで偏微分したものとして、正しいものを以下の中から選べ。

（1） 9x2−2xyz+y2z2	（2） 9x2−2xyz+y2z2+yz3	（3） 3 x3−x2yz+ xy2z2+yz3
（4） 9x2−2x+4yx+3z2	（5） 9x2−2xyz+4y2x2+3yz2

２．次に示す公式のうち、誤っているものはどれか。

（1）運動の第1法則	Ｆ＝ｍａ	F：力　 m：質量　 a：加速度
（2）ボイルシャルルの法則	ｐＶ／Ｔ＝一定	p：圧力　 V：体積　 T：絶対温度
（3）ベルヌーイの式	ｐ／ρｇ＋ｖ2／２ｇ＋ｚ＝一定	p：圧力　 ρ：密度 　ｖ：流速 g：重力加速度　 z：高さ
（4）オームの法則	Ｖ＝ＲＩ	V：電圧　 R：電気抵抗 　I：電流
（5）レイノルズ数	Ｒｅ＝ＶＬ／ν	Re：レイノルズ数 　V：代表速度 L：代表長さ　 ν：動粘度

３．有限要素法に関する以下の記述の中で不適切なものはどれか。

（1） 有限要素法は「Finite Element Method」の日本語訳でその頭文字をとってFEMと呼ばれる場合が多い。
（2） 一つの要素は4つの節点から構成され、一般に要素を小さくすればするほど解析の精度が良いとされる。
（3） 要素内における物理量の分布は内挿関数の分布に従う。
（4） 有限要素法は数値計算に基づく近似解法の一つである。
（5） 節点や要素の配置の仕方は解析者の経験に負うところが大きい。

４．2点A、Bの座標を（2、-2、1）、（-3、1、-4）とするとき原点Oを通る線分OA、OBを2辺とする平行四辺形の面積を求めよ。

（1）√35　　（2）2√14　　（3）3√10　　（4）12　　（5）3√26

５．関数の極限と連続について述べた次の記述のうち誤っているものはどれか。

（1） f（x）がx=aで微分可能であれば、f（x）はx=aで連続である。
（2） f（x）、g（x）がともにx=aで連続の時、f（x）＋g（x）はx=aで連続であるが、f（x）-g（x）は必ずしもx=aで連続とは限らない。
（3） ｌｉｍ_ｘ→ａ｛ｆ（ｘ）｝＝ｍ、ｌｉｍ_ｘ→ａ｛ｇ（ｘ）｝＝ｎならばｌｉｍ_ｘ→ａ｛ｆ（ｘ）±ｇ（ｘ）｝＝ｍ±ｎである。
（4） 二つの連続な関数y=f（u）、u=g（x）の合成関数y=f（g（x））はxの連続関数である。
（5） 関数f（x）が閉区間〔a、b〕で連続で、f（a）＜f（b）であるとすれば、f（a）＜k＜f（b）である任意の数kに対してf（ξ）=kを満たすξが閉区間〔a、b〕に少なくとも一つは存在する。

６．ヤング率Eを表す式はどれか。
　　ここで、L：棒の長さ、A：棒の断面積、P：棒に加わる軸方向荷重、λ：棒の軸方向の伸びあるいは縮み

(1) Ｅ＝Ｐλ／ＬＡ
(2) Ｅ＝ＰＡ／λＬ
(3) Ｅ＝ＰＬ／λＡ
(4) Ｅ＝ＬＡ／Ｐλ
(5) Ｅ＝λＬ／ＰＡ

７．電気抵抗について述べた次の記述のうち誤っているものはどれか。

(1） 電気抵抗Rの導線に電位差Vを与えると、導線中を流れる電流IはI=V/Rである。
(2） 導線の電気抵抗は導線の断面積に比例する。
(3） 金属導体の抵抗は一般に温度の上昇とともに増加する。
(4） 抵抗R₁、R₂を直列に接続した場合、合成抵抗RはR = R₁+R₂と表される。
(5） 半導体ではオームの法則は成立しない。

８．真空中の一辺の長さa（m）の正方形の各頂点に+Q（C）の正電荷を持った点電荷が置かれているとき、正方形の中心に置かれた−2Q（C）の正電荷に働く力は次のうちどれか。
　　ここで、真空中で距離r（m）離れた地点に置かれた二つの点電荷Q₁（C）、Q₂（C）の間に働く力Fは、Ｆ＝ｋＱ₁Ｑ₂/ｒ²と表される。

（1） -ｋ８Ｑ²/ａ²　　　（2） -ｋ４Ｑ²/ａ²　　　（3） 0　　　（4） ｋ４Ｑ²/ａ²　　　（5） ｋ８Ｑ²/ａ²

９．電荷Qを蓄えた静電容量Cのコンデンサーと、電荷2Qを蓄えた静電容量4Cのコンデンサーがある。
　　この二つのコンデンサーを並列に接続したときの静電エネルギーはどれだけか。
　　ここで今回だけのスペシャルヒントとして、静電エネルギーEの公式を示す。電荷Q（C：クーロン）を蓄えた静電容量C（F：ファラデー）のコンデンサーの静電エネルギーE（J：ジュール）は、Ｅ＝1/2・Ｑ²/Ｃと表される。

(1) 3/10・Ｑ2/Ｃ（Ｊ）　　　(2) 1/2・Ｑ2/Ｃ（Ｊ）　　　(3) 3/5・Ｑ2/Ｃ（Ｊ）　　　(4) 9/10・Ｑ2/Ｃ（Ｊ）　　　(5) Ｑ2/Ｃ（Ｊ）

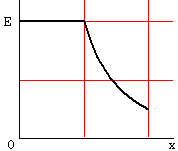
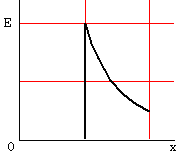
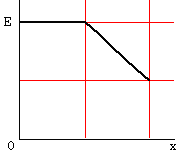
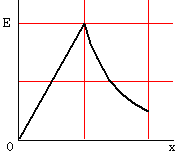
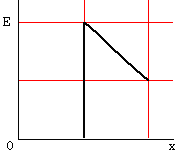
10．真空中にある半径aの導体球に電荷を与えたとき、球の中心からx離れた点の電界の強さEはどのように変化するか。次のうち正しいものを選べ。
　　なお、導体球では電荷は全て球表面に集中すること、また、導体球外の電界は、全電荷が球の中心に集まっていると考えて求めることができる。

(1)	(2)	(3)
(4)	(5)

＜正解＞

1. 正解：1
   xで偏微分するときはyとzは係数扱いとなる。ψ= f ( x , y , z ) = 3 x3−x2yz+ xy2z2+yz3。
   xで偏微分すると、第一項は9x2、第二項は−2xyz、第三項はy2z2、第四項は0と計算される。
   つまり、∂ψ/∂x ＝ 9x2−2xyz+y2z2 と計算される。
   
2. 正解：1
   （1）誤り。この式は運動の第2法則。ちなみに第1法則とは『すべての物体は外力によってその状態を変えられない限り、その静止の状態あるいは一直線の一様な運動の状態をそのまま続ける。』というものである。別名、慣性の法則と呼ぶ。
   
3. 正解：2
   （2）誤り。不規則メッシュを用いることができるので、複雑形状問題に対応しやすい。一要素あたりの節点数は様々なものが可能で、近年では三次元要素もよく使われる。
   
4. 正解：3
   三角形OABの面積Sは
   S=1/2×｜OA→×OB→｜で表される。
   ここで、OA→×OB→はベクトルの外積またはベクトル積という。
   OA→=（x1、y1、z1）、OB→=（x2、y2、z2）、とすると
   OA→×OB→＝（y1×z2−y2×z1 、z1×x2−z2×x1 、x1×y2−x2×y1 ）である。
   ここで、設問に戻る。
   OA→×OB→＝（(-2×-4)−(1×1) 、(1×-3)−(-4×2) 、(2×1)−(-2×-3)）＝（7、5、-4）である。
   ｜OA→×OB→｜ = √(49+25+16) ＝ √90 = 3√10
   平行四辺形の面積は三角形の2倍である。
   ※注意：OA→はベクトルＯＡを表す
   
5. 正解：2
   f（x）、g（x）がともにx=aで連続の時、f（x）±g（x）はx=aで連続である。
   ちなみに（5）は中間値の定理といわれている。
   
6. 正解：3
   フックの法則は σ = Eε である。
   σは応力であり、P/Aで表される。
   また、εはひずみであり、�儉/L = λ/Lで表される。
   つまり、フックの法則はP/A=Eλ/Lと表され、これをEの式に示すと、
   E = PL/λA
   
7. 正解：2
   導線中を流れる電流Iは電位差Vに比例する。電気抵抗Rとすると、導線中を流れる電流IはI=V/Rである。電気抵抗Rは導体の種類や寸法によって決まる定数である。Rの単位は（V/A）となるが、これをオーム（Ω）と表す。I=V/R の関係をオームの法則という。
   導線の抵抗は長さに比例し、断面積に反比例する性質がある。
   長さl（m）、断面積S（m2）の一様な導線の抵抗RはR=ρｌ/S（Ω）で表される。
   ここで、ρは抵抗率といい、導線の材質によって決まる定数である。単位は（Ω・m）
   半導体や絶縁体ではオームの法則は成り立たないが、おおよその抵抗率は
   　金 属：10^-8〜10^-7（Ω・m）
   　半導体：10^-4〜10⁶（Ω・m）
   　絶縁体：10⁸〜10¹⁶（Ω・m） である。
   導体の抵抗は一定不変なものではなく、温度によって変化する。金属導体の抵抗は一般に温度の上昇とともに増加する。
   t = t₁（℃）における抵抗をR₁とし、t = t₂（℃）における抵抗が
   R₂ = R₁[1+α1(t₂− t₁)]
   と表されるとき、α1を t₁（℃）における抵抗の温度係数という。各種金属の抵抗率と抵抗の温度係数を表に示す。表にあるようにマンガニンの抵抗と温度係数は他の金属に比べて極めて小さく、標準抵抗器の抵抗材料として使用されている。
   金属以外の導体や半導体では、温度の上昇とともに抵抗が下がるのが普通であり、抵抗の温度係数は負となる。半導体を材料としたサーミスタは抵抗の温度係数が大きく、温度センサとして用いられる。
   抵抗R₁、 R₂、R₃を直列に接続した場合、合成抵抗RはR = R₁+ R₂2+R₃と表される。
   また、並列に接続した場合、1/R=1/R₁＋1/ R₂＋1/R₃が成立する。
   
   
8. 正解：3
   真空中で距離r（m）離れた地点に置かれた二つの点電荷Q1（C）、Q2（C）の間に働く力Fは、
   F=ｋ・Q1Q2/ｒ²（N） と表される。Q1、Q2が同符号であれば反発力が働き、異符号であれば吸引力が働く。この式は実験でクーロンによって定量的に発見されたので、この力はクーロン力あるいは静電力と呼ばれる。また、この式の関係をクーロンの法則という。
   ここで、kは定数で、真空中ではｋ＝1/(4πε₀)＝9.0×10⁹である。
   ε₀は真空中の誘電率と呼ばれ、その値はε₀ = 8.85×10^-12（F/m）である。
   さて、問題であるが、正方形の真ん中に置かれた点電荷は4方向に同じ力で引っ張られる。つまり、点電荷に働く力は0となる。
   
9. 正解：4
   並列接続の静電容量は C₀ = C₁+C₂+・・・・ と表される。
   ちなみに直列接続の静電容量は 1/C₀ = 1/C₁+1/C₂+・・・・ である。
   このことからC₀ = C+4C = 5Cと計算される。
   次に電荷Qは単純にQ₀ = Q+2Q = 3Qと計算される。
   静電エネルギーはE=1/2・Q²/C＝1/2・9Q²/(5C)＝9/10・Q²/C（J）と計算される。
   
   
10. 正解：2
    導体球の中心からx離れた場所での電界はE=Q/(4πε₀x²)=（V/m）となる。つまり距離の二乗に反比例する。
    次に導体球内部を考える。電荷は導体球の表面に集中しているので内部は無電荷である。よって内部には電気力線はない。すなわち電界E = 0である。