1-1-1�@���}�̂悤�Ȍn�ɂ����āA�e�\���v�f�̐M���x���AR1��0.9�AR2��0.8�AR3��0.5�AR4=0.7�̂Ƃ��A���̌n�̐M���x�����߁A���̒�����ł��߂����̂�I�ׁB
(1) 0.25�@�@(2) 0.60�@�@(3) 0.73�@�@(4) 0.85�@�@(5) 0.91
�Z�p�m��ꎟ�����@����19�N�x�@��b�Ȗ�
���E�����E���
���Z�p�m����\�̐����ɂ��āA�Վ��f���ł̏�������쐬���܂����B
�@�٘_����Ȃǂ���܂�����A���[���ɂĂ��肢���܂��B
| ��b�Ȗڐ����ꗗ | |||||||||||||
| ��1�Q�F�v�E�v�� | ��2�Q�F���E�_�� | ��3�Q�F��� | ��4�Q�F�ޗ��E���w�E�o�C�I | ��5�Q�F�Z�p�A�� | |||||||||
| 1-1-1 | 4 | 1-2-1 | 5 | 1-3-1 | 4 | 1-4-1 | 2 | 1-5-1 | 1 | ||||
| 1-1-2 | 2 | 1-2-2 | 3 | 1-3-2 | 3 | 1-4-2 | 5 | 1-5-2 | 2 | ||||
| 1-1-3 | 5 | 1-2-3 | 4 | 1-3-3 | 3 | 1-4-3 | 2 | 1-5-3 | 4 | ||||
| 1-1-4 | 2 | 1-2-4 | 1 | 1-3-4 | 4 | 1-4-4 | 3 | 1-5-4 | 4 | ||||
| 1-1-5 | 3 | 1-2-5 | 3 | 1-3-5 | 1 | 1-4-5 | 1 | 1-5-5 | 5 | ||||
1�Q�@�v�E�v��ɖ₷����́@(�S5��肩��3����I����)
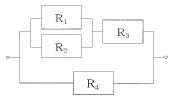
1-1-1�@���}�̂悤�Ȍn�ɂ����āA�e�\���v�f�̐M���x���AR1��0.9�AR2��0.8�AR3��0.5�AR4=0.7�̂Ƃ��A���̌n�̐M���x�����߁A���̒�����ł��߂����̂�I�ׁB

(1) 0.25�@�@(2) 0.60�@�@(3) 0.73�@�@(4) 0.85�@�@(5) 0.91
������4
����q�\���̌n�̐M���x�́A�������n����傫���n�ւƏ��Ɍv�Z���Ă����܂��B�܂�AR4�`�iR3�`�iR1�`R2�j�j�ƂȂ�킯�ł��B
�܂�R1��R2�͕���ɂȂ��Ă��܂��B�ł�����M���x�͂��ꂼ��̃G���[���|�����킹�����̂�1���猸�����l�ɂȂ�܂��B
R1�̐M���x��0.9�A����ăG���[��1-0.9��0.1�BR2�͐M���x0.8�ɂ��G���[��0.2�B������|�����킹���0.02�ŁA1���猸����0.98�B���̂��Ƃ́A
�@�@1-�i1-0.9�j�~�i1-0.8�j
�Ƃ����`�Ŏ��ɕ\�킹�܂��B
���āA�����R3�͍��x�͒���ɂȂ��Ă��܂��B����͐M���x���|�����킹�����̂ł���AR3�̐M���x��0.5�ł�����A0.98�~0.5��0.49�ƂȂ�܂��B
�Ō�ɂ����R4�͕���ɂȂ�܂��B����ăG���[�̊|�����킹�Ă���R3�̑��͐M���x��0.49�Ȃ̂ŃG���[��1-0.49��0.51�BR4�̐M���x��0.7�Ȃ̂ŃG���[��0.3�B����āA0.51�~0.3��0.153�B�����1���猸����̂�0.847�ƂȂ�܂��B�ȏ�̌v�Z�͑S���ÎZ�łł��܂��B
����Ĉ�ԋ߂��̂�(4)��0.85�ƂȂ�܂��B
1-1-2�@���鐻�i�̐����H���ɂ����Č������w����{����ƁA�s��̔�������m����1�^�i�w�{1�j2�ɂȂ�Ɛ��肳�����̂Ƃ���B�����ɗv�����p���i30�w�j���~�ł���A�s��̔����ɂ�鑹�Q��1,875���~�Ɛ��肳���Ƃ���ƁA�����w������ɐݒ肷��Α���p���ŏ��ƂȂ邩�����̒�����I�ׁB
(1)�@3��@�@�@(2)�@4��@�@�@(3)�@5��@�@�@(4)�@6��@�@�@(5)�@7��
������2
�g���C�A���i���Ă͂߁j�v�Z���J��Ԃ��Ă������܂����A�ȉ��̎菇�ŋ��ȏ��ǂ���̕��@�ʼn����Ă݂܂��B
1-1-3�@�n�k���ɂ́A�}�|1�̂悤�ɐ��������̗h��ɂ���Č��݂Ɋ����͂��\�����ɍ�p����B�͂�ƒ����爽�鍜�g�\���������̕������ꍇ�ɂ́A���ʓI�ɐ}�|2�̂悤�ɂǂ��炩�̕����Ɂu�}�b�`�����Ԃ��悤�ȁv�j��i����f�j��j�����邱�Ƃ�����B�͂�ƒ��ň͂܂ꂽ�ǂ̕������A�����^���Ȃǂ̂Ђъ��ꂪ�������₷���ޗ��ő����Ă��āA�S�Ȃǂ̕⋭���Ȃ����̂Ƃ���B���̕ǂ̕������u�P������f��ԁv�i����f���݂͂̂��͂�ƒ�����`������j�ɂ���A�Ђъ��ꂪ��������͂ƒ�����������ɔ���������̂Ƃ���Ȃ�A���g�̔j��ɐ旧���Č����ɔ�������ł��낤�Ђъ���́A���_��ǂ̂悤�Ȃ��̂ɂȂ�Ɨ\�z����邩�B�ł��K�Ȃ��̂��@�`�D�̒�����I�ׁB
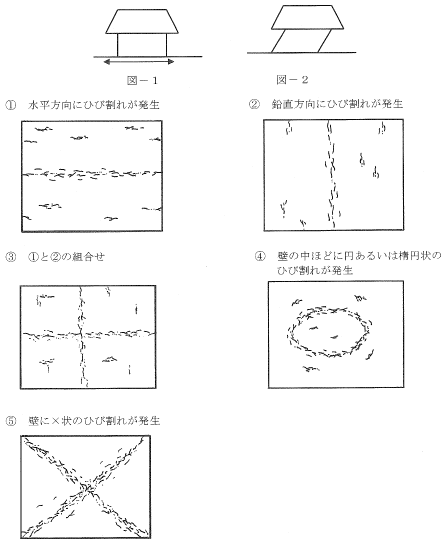
������5
| �n�k���ɂ́A�Ɖ����}2�̂悤�Ȍ`�ɕό`���悤�ƍ��E�ɗh��邽�߁A�������͂ƈ��k���͂͐}�̂悤�ɑΊp�������ɓ����܂��B��蕶�ɂ���悤�ɁA�u�Ђъ��ꂪ��������͂ƒ�����������ɔ����v����̂ŁA�I����(5)�̂悤�ȑΊp�������悤�ȋT�ł��܂��B���ہA��_��k�Ђł͂��������T�ł��Ă��܂��B | 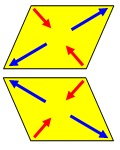 |
1-1-4�@�z�^�Љ�Ɋւ���鎟�̋L�q�́m�@�A�@�n�`�m�@�G�@�n�ɓ��錾�t�Ƃ��čł��K�Ȃ��̂�(1)�`(5)�̒�����I�ׁB
�@�z�^�Љ�Ƃ́A���1�ɐ��i�����p�������ƂȂ邱�Ƃ�}�����A��2�ɔr�o���ꂽ�p�������ɂ��Ă͂ł��邾�������Ƃ��ēK���ɗ��p���A�Ō�ɂǂ����Ă����p�ł��Ȃ����͓̂K���ɏ������邱�Ƃ��O�ꂳ��邱�Ƃɂ����������A�V�R�����̏���}������A���ւ̕��ׂ��ጸ�����Љł���B
�@�p�����̔������̂�}�����邱�Ƃ��m�@�A�@�n�A��������g�p���ꂽ���i�╔�i�A�e�퓙���Ďg�p���邱�Ƃ��m�@�C�@�n�A�p���������ė��p���邱�Ƃ��m�@�E�@�n�Ƃ����B������3�̓��������Ƃ���3�q�ƌĂ�ł���B
�@���ޗ��̎悩�琻���A���ʁA�g�p�A�p���Ɏ���܂ł̐��i�̈ꐶ�U�ŁA���ɗ^����e���͂��A�����]�������@���m�@�G�@�n�Ƃ����B
(1)�@�i�A�j���T�C�N���@�@�i�C�j�����[�X�@�@�i�E�j���f���[�X�@�@�i�G�j�[���E�G�~�b�V����
(2)�@�i�A�j���f���[�X�@�@�i�C�j�����[�X�@�@�i�E�j���T�C�N���@�@�i�G�j���C�t�T�C�N���E�A�Z�X�����g
(3)�@�i�A�j���T�C�N���@�@�i�C�j���f���[�X�@�i�E�j�����[�X�@�@�@�i�G�j���C�t�T�C�N���E�A�Z�X�����g
(4)�@�i�A�j���f���[�X�@�@�i�C�j�����[�X�@�@�i�E�j���T�C�N���@�@�i�G�j�}�e���A���E�t���[���
(5)�@�i�A�j���T�C�N���@�@�i�C�j���f���[�X�@�i�E�j�����[�X�@�@�@�i�G�j�}�e���A���E�t���[���
������2
�m�����ł����A�i�A�j�`�i�E�j�͏펯���x���̒m���ł��B�u���f���[�X�E�����[�X�E���T�C�N���v��1�̒P��݂����Ȃ��̂ł��ˁB
���̎��_�Ő�����2��4�ɍi�荞�܂�܂��B
�i�G�j�ɂ��ẮA
�@�[���E�G�~�b�V�����F���Ƃɔ����Ĕ�������p�����i�G�~�b�V�����j���[���ɂ�����g��
�@���C�t�T�C�N���E�A�Z�X�����g�F���i�̌��ޗ��̎悩�琻���E���ʁE�g�p�E�p���Ɏ��鐻�i�̃��C�t�T�C�N���ɓn������ׂ̗\���]��
�@�}�e���A���E�t���[��́F���m�i���ɗL�Q�����j�̗���ɒ��ڂ��āA������ʓI�ɕ\�����A�]���E��͂����@
�ł����A���������֘A�p��Ƃ��Ă͊�b�I�Ȃ��̂ł��B
1-1-5�@����{�݂̌v��ăA�`�I������B�����̌v��Ăɂ��{�݂̌��݂ɂ���ē�����։v���A�����̎Љ������a,b,c�ɂ��\1�̂悤�ɕω�������̂Ƃ���B�܂��A���ꂼ��̌v��Ăɗv���錚�ݔ�p���\2�Ɏ������Ƃ���Ƃ���B�����̎Љ�������̔����m�����A���ꂼ��a��60��,b��30��,c��10���Ɨ\�������ꍇ�A���҂���鉿�l�i���։v���p�j���ł��傫���Ȃ�v��Ă�(1)�`(5)�̒�����I�ׁB
| �\1�i�P�ʁF���~�j | �@�@�@ | �\2�i�P�ʁF���~�j | ||||||||||||||||||||||||||||||||||||
|
|
(1)�@�A�@�@�@(2)�@�C�@�@�@(3)�@�E�@�@�@(4)�@�G�@�@�@(5)�@�I
������3
�܂��͖�蕶�̈Ӗ��ɓ���܂��傤�B
���Ƃ��Όv��ăA�̏���a�ɒ��ڂ��܂��B���҂ł���։v��5���~�ł����A���ꂪ��������m����60���ł��B����āA���Ғl��5���~�~60����3���~�ƂȂ�܂��B���l��b�Ac�ɂ��Ă����Ғl���v�Z����ƁAb��4���~�~30����1.2���~�A����3���~�~10����0.3���~�ƂȂ�A���v4.5���~�ƂȂ�܂��B�����Č��ݔ�p��3���~������̂ł�����A��������4.5���~�|3���~��1.5���~�����Ғl�ɂȂ�܂��B�ЂƂ܂Ƃ߂ɂ��ď����ƁA5*0.6+4*0.3+3*0.1-3��1.5�ƂȂ�܂��B
�Ȃ��A�葁�����ɂ́u�~0.6�v�ȂǂƂ����Ɂu�~6�v�Ƃ����悤�ɂ��ĒP�ʂ��u���~�v�ł͂Ȃ��u�疜�~�v�ɂ��Ă��܂��Ɗy�ł��B���̏ꍇ�A�v��ăA�̊��Ғl��15�ƂȂ�܂��B
���l�Ɍv��ăC�`�I�ɂ��Čv�Z����ƁA
�@�i�C�j4*6+6*3+7*1-40��9
�@�i�E�j3*6+7*3+8*1-30��17
�@�i�G�j6*6+4*3+3*1-40��11
�@�i�I�j7*6+5*3+4*1-60��1
�ƂȂ�A�i�E�j�̊��Ғl���ł������Ȃ�܂��B
�����Ғl�̐�Βl�����߂�̂ł͂Ȃ��㏞�]��������̂��ړI�ł�����A�P�ʂ����ł��������ƂŁA�����ł������y�ɂł�����@���g���̂�����ł��B�u�~6�v�Ȃ�ÎZ�ł������Ƃł��܂����A�u�~0.6�v�Ƃ��u�~60�v���Ǝ��Ԃ������邩�d���]�v�ɑ��삵�Ȃ���Ȃ�܂���B
2�Q�@���E�_���Ɋւ�����́@(�S5��肩��3����I����)
1-2-1�@���{�̎w���g���A���ꂼ��̋Ȃ�����ԂƐL������Ԃ��l����B���Ƃ���2�{���g�����ꍇ�ɂ́A����4�ʂ�̏�Ԃ�\���ł���B
| �l�����w | �e�w |
| �Ȃ��Ă��� | �Ȃ��Ă��� |
| �Ȃ��Ă��� | �L���Ă��� |
| �L���Ă��� | �Ȃ��Ă��� |
| �L������ | �L������ |
10�{�̎w���g���ꍇ�ɂ́A5�{�̎w���g���ꍇ�Ɣ�ׂĕ\���ł����Ԃ̐��͉��{�ɂȂ邩�B
(1)�@2�{�@�@(2)�@4�{�@�@(3)�@8�{�@�@(1)�@16�{�@�@�@(5)�@32�{
������5
����̓r�b�g�̏��ʂɊւ�����ł��B
�u�w�̋Ȃ�����ԂƐL������ԁv�̓I���E�I�t�A�܂�0��1�Ƃ����f�W�^���M���́u2�ʂ�̏�ԁv�Ɠ����ł��B
�����āu2�{���g�����ꍇ�ɂ́A����4�ʂ�̏�Ԃ�\���ł���v�Ƃ����̂́A22��4�Ƃ������Ƃł��B���̏ꍇ�́u2�{�v�́u2��v�Ƃ������Ƃ�\�킵�܂��B�܂�A�i�w���Ȃ������/�L������Ԃ�2�ʂ�j^�i2�{�̎w�j�Ƃ������ƂɂȂ�܂��B�ł�����w3�{���g����23�A�܂�8�ʂ�̏�ԕ\�����ł��܂���4�{�Ȃ�24�A�܂�16�ʂ�̕\�����ł��܂��B
���̂悤�ɁA�Ȃ���/�L�����A0��1�̂悤��2�ʂ�̏�Ԃ�\���ł���v�f��n�W�܂��ĕ\���ł����Ԃ̐��i���ʁj�́A2n�ƂȂ�܂��B������un�r�b�g�v�Ƃ����܂��B
���������āA10�{�̎w���g����10�r�b�g��210�A5�{�Ȃ�5�r�b�g��25�̏��ʂɂȂ�܂��B
2m��2n��2m-n�ł�����A210��25��210-5��25��32�ƂȂ�܂��B
���r�b�g�Ɋւ�����ł���Ƃ������Ɓi���邢�͏��ʁ�2n�ł���Ƃ������Ɓj���킩��A�v�Z�͍��Z���w���x���ł��B
1-2-2�@�f�[�^���l�b�g���[�N�œ`������ꍇ�ɂ́A�m�C�Y���̌����ňꕔ�̃r�b�g�����]����`����肪��������\��������B�`���������o���邽�߂ɁA�f�[�^�̖�����1�r�b�g�̕�����t�����ē`��������@���l����B�t������r�b�g�̒l�́A���̃f�[�^�̒��̒l���u1�v�̃r�b�g�̐��������ł���u0�v�A��ł���u1�v�Ƃ���B���Ƃ��A���̃f�[�^���u1001011�v�Ƃ���7�r�b�g�ł���Ƃ��A�l���u1�v�̃r�b�g��4�ŋ����ł���B����āA�t������r�b�g�́u0�v�ł���A�u10010110�v�Ƃ���8�r�b�g��`������B���̂Ƃ��A���������̂����̒�����I�ׁB
(1)�@�f�[�^�̒���1�r�b�g�����]�������Ƃ����o���邽�߂ɂ́A���̃f�[�^��8�r�b�g�ȉ��łȂ���Ȃ�Ȃ��B
(2)�@�f�[�^�̒���1�r�b�g�����]�������Ƃ����o���邽�߂ɂ́A���̃f�[�^��2�r�b�g�ȏ�łȂ���Ȃ�Ȃ��B
(3)�@�f�[�^�̒���2�r�b�g�����]�����ꍇ�ɂ́A�`���������o�ł��Ȃ��B
(4)�@8�r�b�g�̃f�[�^�̒���1�r�b�g�����]�����ꍇ�ɂ́A�ǂ̃r�b�g�����]�����������ł���B
(5)�@�f�[�^�ɂ���Ă͕t������r�b�g�̒l�����߂��Ȃ����Ƃ�����B
������3
�r�b�g�Ɋւ���ݖ�ŁA�����ł͒l���u1�v�ł���r�b�g���𐔂��A�������ǂ����ŕt������l��0��1�����f���Ă��܂��B
����I����������ƕp�ɂɏo�Ă��錾�t���u�r�b�g�����]�v�ł��ˁB�r�b�g���u���]����v�Ƃ́A1�Ȃ�0�ɁA0�Ȃ�1�ɕς���Ă��܂����Ƃł��B�܂�A�l���u1�v�ł���r�b�g�����A���]�����r�b�g�������������܂��B
����1�������]�����Ƃ��܂��傤�B0����1�ɔ��]�����̂ł���Βl���u1�v�̃r�b�g����1�����܂��B1����0�ɔ��]�����̂ł����1����܂��B
3���Ƃǂ��ł��傤�B3�Ƃ�0����1�ɔ��]�����̂ł���Βl���u1�v�̃r�b�g����3�����܂��B2��1�ɁA1��0�ɔ��]�����̂ł���A���E����2-1��1�����܂��B1��0�ɁA2��1�Ȃ�1-2��-1������A�܂�1����܂��B3�Ƃ�0�ɔ��]�����Ȃ�3�ւ�܂��B
���̂悤�ɁA���]�����r�b�g������Ȃ�A�l���u1�v�ł���r�b�g���͊�����������܂��B�܂�A�l���u1�v�ł���r�b�g�̐��͋����^�������ւ��܂��B����čŌ�ɕt�������1�r�b�g�̒l�́u0�v���u1�v���邢�́u1�v���u0�v�̂悤�ɕω����܂��B
����������ƁA���]�����r�b�g����2�̏ꍇ�A2�Ƃ�1�ɔ��]�����Ȃ�l���u1�v�̃r�b�g����2���A1��1�ɁA����1��0�ɔ��]�����Ȃ瑊�E���ĕω��Ȃ��A2�Ƃ�0�ɔ��]�����Ȃ�2���ƂȂ�܂��B���l�ɔ��]�����r�b�g����4�̏ꍇ�A1�ɔ��]�����r�b�g���F0�ɔ��]�����r�b�g����4�F0�Ȃ�l���u1�v�̃r�b�g����4���A3�F1�Ȃ�2���A2�F2�Ȃ�v���X�}�C�i�X0�A1�F3�Ȃ�2���A0�F4�Ȃ�4���ƂȂ�܂��B
���̂悤�ɁA���]�����r�b�g���������Ȃ�A�l���u1�v�ł���r�b�g���͋��������������܂��B�܂�A�l���u1�v�ł���r�b�g�̐��͋����^�������ւ��܂���B����čŌ�ɕt�������1�r�b�g�̒l�͕ω����܂���B
�ȏ�̂悤�ɁA���]�r�b�g������ł������ꍇ�́A�Ō�ɕt�������1�r�b�g�̒l���ω��������ǂ����ׂ邱�ƂŁA���]���N���������ǂ�����m�邱�Ƃ��ł��܂��B����������ƁA���̂悤�ȕ��@�ł́A���]�r�b�g������ł������ꍇ������������o�ł��Ȃ����ƂɂȂ�܂��B
�ȏ�܂��đI���������Ă����܂��B
(1)��(2)�͌��̃f�[�^�̃r�b�g���ɂ��ďq�ׂĂ��܂����A���]�r�b�g��������������Ō��o�\���ǂ������܂�̂ł�����A�f�[�^�̃r�b�g���͔��]���o�ɂ͊W����܂���B����Č��ł��B
(3)�͏�L�ɂ�萳�����L�q�ƂȂ�܂��B
(4)�́A���]�̗L���������o�ł��Ȃ����Ƃɂ��A���ł��B
(5)�́A�t���r�b�g�l�́A�l���u1�v�̃r�b�g��������������Ō��܂�܂�����A��ł������ł��Ȃ����Ƃ����̂͑��݂��܂���B����Č��ł��B
�������Ŏ��グ���Ă���r�b�g�t���ɂ��`����茟�o���@�́u�p���e�B�`�F�b�N�v�ƌ�������̂ŁA1�ł���r�b�g���̋����E������ڂ��čŌ�ɏ�������1�r�b�g�̂��Ƃ��p���e�B�r�b�g�Ƃ����܂��B���ۂ̓`���ł́A���̓p���e�B�r�b�g�ȊO�̃r�b�g�i���{�́j�ׂĒl��1�ł���r�b�g�𐔂��A������p���e�B�r�b�g�Əƍ����܂��B���v���Ȃ���f�[�^�`���ɃG���[���������Ɣ��f���A���葤�ɍđ���v�����܂��B
��茟�o�Ƃ��Ă͂����Ƃ��|�s�����[�ȕ��@�ŁA�R���s���[�^�����̉�H�ԃf�[�^�]���A�ʐM������g�����R���s���[�^���m�̒ʐM�ɕ��L�����p����Ă��܂����A�I����(3)�̂悤�ȒZ��������܂��B
1-2-3�@�@�B�`,�a��p���čޗ��o,�p,�q�����H�������B�ޗ��͂�������@�B�`,�a�̏��ɉ��H���Ȃ���Ȃ�Ȃ��B
�@�B�`�ōޗ��o,�p,�q�����H����̂ɗv���鎞�Ԃ͂��ꂼ��10��,20��,13���ł���A�@�B�a�ōޗ��o,�p,�q�����H����̂ɗv���鎞���͂��ꂼ��12��,15��,5���ł���B
�e�@�B�͈�x��1�̍ޗ��������H�ł��Ȃ��B�@�B��1�̍ޗ��̉��H���n�߂���A���̉��H�𒆒f���邱�Ƃ͂ł��Ȃ��B2��̋@�B�́A�قȂ�ޗ������H����̂ł���A���s���Ďg�p�ł���B�ޗ����@�B�Ԃ��ړ����鎞�Ԃ�i���ɗv���鎞�Ԃ͍l���Ȃ��Ă悢�B
�@�B�`�A�a�̂�����ɂ����Ă��ޗ����o,�p,�q�̏��ɉ��H����Ƃ�����A�ŏ��̉��H���n�܂��Ă���Ō�̉��H���I��܂ł̎��Ԃ̍ŏ��l�͂����炩�B���̒�����I�ׁB
(1)�@32���@�@(2)�@43���@�@(3)�@47���@�@(4)�@50���@�@(5)�@75��
������4
�H���Ǘ��Ɋւ�����ł��B
�킩��₷���悤�Ƀo�[�`���[�g�ɂ��Ă݂܂��傤�B
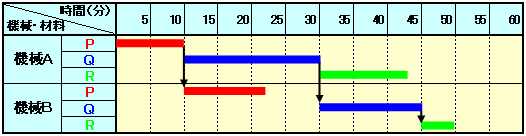
�@�BA���@�BB�̏��ʼn��H���Ȃ���Ȃ�Ȃ��̂ŁA�܂��@�BA�ōޗ�P�����H���܂��B���̌�@�BA�ł͍ޗ�Q�̉��H���n�߁A�@�BB�ł͍ޗ�P�̉��H���n�߂܂��B
�@�BA��20���������čޗ�Q�����H���A���ꂪ�I�������ޗ�R�ɂƂ肩����܂��B������43���ʼn��H���I���܂��B
����A�@�BB�͍ޗ�P�̉��H��12���ŏI���̂ł����A�u2��̋@�B�́A�قȂ�ޗ������H����̂ł���A���s���Ďg�p�ł���v�Ƃ������������Ă��܂�����A�@�BA���ޗ�Q�����H���I����̂�҂��˂Ȃ�܂���B������13���҂�����ɍޗ�Q�����H���n�߁A45���ɏI���܂��B���̎��_�ŋ@�BA�͂����S�ޗ��̉��H���I���Ă��܂�����A����ɉe������邱�ƂȂ������ɍޗ�R�̉��H�ɓ���܂��B������5���Ԃʼn��H���I���A50���ɑS�H�����I�����܂��B
�ȏ�ɂ��A�I����(4)�������ƂȂ�܂��B
�o�[�`���[�g�ł͂Ȃ��A���[�_�C���O�����Ő�������Ɖ��}�̂悤�ɂȂ�܂��B�����Ō����_3�`�����_4�A�����_5�`�����_6�̖�j���̓_�~�[�ł��B
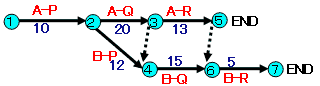
�C�܂Ň@���A���C�Ƃ����22���ł����A�B��A-Q�H�����I����Ă��邱�Ƃ�B-Q�H���J�n�̏����ɂȂ��Ă��܂�����A�@���A���B��30�������Ă���łȂ��ƊJ�n�ł��܂���B
���ǁA�@���A���B���C���E���F�Ƃ����o�H���N���e�B�J���p�X�ƂȂ�A10+20+15+5��50�����ŏ����ԂƂȂ�܂��B
1-2-4�@����ϕ�������A�����������̉������߂��肷��Ƃ��ɁA���������ʼn������߂�̂łȂ����l�I�ɉ������߂�ꍇ�́A�덷��������B�덷�ɂ��Ă̋L�q���́m�@�@�n�ɓ��鎚��̑g�����Ƃ��čł��K�ȑg������(1)�`(5)�̒�����I�ׁB
�m�@�A�@�n�̓R���s���[�^�ň������l���L�����̃r�b�g�ŕ\��������Ƃɂ��덷�ł���B
�m�@�C�@�n�͖{���͖��������琬������L�����̎��Œu�������邱�Ƃɂ��덷�ł���B
| �i�A�j | �i�C�j | |
| (1) | �ۂߌ덷 | �ł���덷 |
| (2) | ���Ό덷 | �ł���덷 |
| (3) | ������ | �ۂߌ덷 |
| (4) | ������ | ��Ό덷 |
| (5) | �ۂߌ덷 | ��Ό덷 |
������1
�R���s���[�^�����l�f�[�^�������Ƃ��A�ǂ̂悤�ɂ��ă������Ɋi�[���Ă���̂ł��傤���B
�R���s���[�^����{�I�Ɉ�������́A�d��������Ă��邩���Ȃ����A�܂�ON/OFF��2��ނ̏��i�f�W�^�����j�����ł��B
�����ǂ���ł�1��0���������܂���B�����ŁA���l���i�[���邽�߂́u���ꕨ�v���������p�ӂ��܂��B���Ƃ���
�@�@����������������
���̂悤�Ɂu���v��8�p�ӂ����Ƃ��܂��B�S���̔����J���̏�ԁi�S���̌��̒l���[���̏ꍇ�j�́A���l��0�ɂȂ�܂��B
���l�u1�v�́A
�@�@����������������
�̂悤�Ɉ�ԉ��̌��Ɂu1�v�������Ă��܂��B�i�d��������Ă��܂��j
���l��������āu2�v�ɂȂ�ƁA�ꌅ�ڂɂ͂�������܂���A
�@�@����������������
�̂悤�ɓڂɁu1�v������A�����Ɉꌅ�ڂ́u0�v�ɂȂ��Ă��܂��B
����ɐ��l�������āu3�v�ɂȂ�ƁA
�@�@����������������
�̂悤�ɁA����Ɉꌅ�ڂɁu1�v������܂��B�ȉ��A
�@�@�����������������@����4
�@�@�����������������@����5
�@�@�����������������@����6
�@�@�����������������@����7
�@�@�����������������@����8
�Ƃ����悤�ɂȂ�܂��B
�����ŁA�����u0�v�A�����u1�v�Ɠǂݑւ���ƁA
�@���l1������������������������00000001���@�@�@1
�@���l2������������������������00000010���@�@10
�@���l3������������������������00000011���@�@11
�@���l4������������������������00000100���@100
�@���l5������������������������00000101���@101
�@���l6������������������������00000110���@110
�@���l7������������������������00000111���@111
�@���l8������������������������00001000��1000
�ƂȂ�܂��B����́A���ꂼ��̐��l��2�i���ŕ\�������l�ł��B���̂悤�ɁA�R���s���[�^�Ōv�Z����ꍇ�ɓ��͂���10�i���́A�R���s���[�^�����ł�2�i���ɕϊ�����ă������Ɋi�[����܂��B
�y�ۂߌ덷�z
����10�i������2�i���ւ̕ϊ��̍ہA2�i���ł�������\���鐔�l�i4�i22�j�A0.5�i2-1�j�A0.75�i2-1+2-2�j�Ȃ�2n�ŕ\���鐔�l�j�͐��m�Ȓl�ƂȂ�܂����A����ȊO�̑啔���̐��l�͖��������ɂȂ�܂��B
�������R���s���[�^�̃������Ȃ�L�����u�͗L���ł�����A�P�̐��l�Ɋ���U���r�b�g�����L���ƂȂ�܂��B���ꂪ�L�������ł��B�R���s���[�^�́A���������L���ł��邪�䂦�A�L�������ɂ͎����Ɛ������ł���̂ł��B
���̂��߁A2�i���ւ̕ϊ��͗L�������܂łőł����A����ȍ~�͐�グ�E��̂āE�l�̌ܓ��E�̘Z���Ȃǂɂ��[����������A�ۂ߂��܂��B
���Ƃ��Ή��̗�ł́A�R���s���[�^�ɓ����悤�ɑł�����0.5��2-1�ł�����2�i���ł�10-1��0.1���Đ��m�Ɍv�Z�ł��A�R���s���[�^�ɂ͐��m�ɓ��͂���܂����A0.1��2�i���ł͖��������ƂȂ�A�r���Ōv�Z���ł����܂��B���̂��߁A�R���s���[�^�ɓ��͂��ꂽ���l�͐��m�ɂ�0.1�ł͂Ȃ��Ȃ�܂��B
| 10�i�� | 2�i�� | �R���s���[�^���͒l | ||
| 0.1 | �� | 0.0001100110011001100110011001���� | �� | 0.1 |
| |�@�@ �@�� 24�r�b�g ���@�@�@|���v�Z�� | ||||
| 0.5 | �� | 0.1 | �� | 0.5 |
���̂��߁A�����̐��l���g���ČJ��Ԃ��v�Z������ƁA�덷���ݐς��Ă������ƂɂȂ�܂��B
| ���l | X=0.1000 | X=0.5000 | ||
| �ݘa�� | �v�Z�l | ���m�l | �v�Z�l | ���m�l |
| 1,000 | 99.999 | 100 | 500 | 500 |
| 10,000 | 999.903 | 1,000 | 5,000 | 5,000 |
���̌덷���ۂߌ덷�ł��B�܂�A���l�i�����j��L�������̃r�b�g���Ƃ��Ċi�[���邽�߂ɐ�����덷�ł��B
�ł��P���ȗ�Ƃ��ẮA�d��Ɂu10�v�u���v�u3�v�u���v�Ɠ��͂��Ă��Ƃ��u3.3333333�v�Ƃ�������Ɂu�~�v�u3�v�u���v�Ɠ��͂���Ɠ�����10�ł͂Ȃ��u9.9999999�v�ɂȂ錻�ۂ��ۂߌ덷�ł��B
�y�������z
�L������8���Ł�1250�����1249�������Ă݂܂��傤�B�܂�A12500.5�|12490.5�ł��ˁB
�@12500.5��35.35533906�����@���@35.355339�@�Ɋۂ߂��ă������Ɋi�[�i�����Ŋۂߌ덷�������Ă���j
�@12490.5��35.34119409�����@���@35.341194�@�Ɋۂ߂��ă������Ɋi�[�i�����Ŋۂߌ덷�������Ă���j
�������Ɋi�[���ꂽ�ۂߌ덷�����������l���m�Ō��Z������ƁA
�@35.355339-35.341194��0.014145
�ƂȂ��āA�L��������5���Ɍ����Ă��܂��܂����B���ꂪ�������ŁA�l���قړ������ۂߌ덷�������l�ǂ����̌��Z���s�����ꍇ�A�L�������������Ă��܂����ۂł��B
���̏ꍇ�A���������_�v�Z�ł́A0.014145��0.14145E-01�Ƃ����悤�ɂׂ�������Ɏ����Ă��邱�ƂŃ������i�[��̏����_�ʒu���ړ������Ă��܂��܂��B���Ƃ��ƃ������ɂ�8�����́u���v���p�ӂ��Ă���܂�����u0.14145�v�̌��ɂ͂܂�������ɂ�������炸�A�����ɂ́u0�v�������I�ɓ�����āA����ȉ��̌��̐��l�͂Ȃ��Ȃ��Ă��܂��A�����Ɍ덷�����܂�܂��B
�y�ł���덷�z
���Ƃ��̒l���2�̒l�Ƃ����������������v�Z����Ƃ��܂��B�v�Z�𑱂���ƌv�Z�l�͂ǂ�ǂ�^�̒l�ɋ߂Â��Ă����܂����A���̌��ʂ��i�[����ϐ��ɂ��Ă����������ʂ��琧�������L�������A���邢�͂���قǂ̐��x��K�v�Ƃ��Ȃ��Ȃǂ̃v���O���}���̈ӎv�Ȃǂɂ��A�����𑱂���ΐ��x���悭�Ȃ�ɂ�������炸�A�r���Ōv�Z��ł���ꍇ�A�ł������Ƃ��납���́u�v�Z�����𑱂���ΎZ�o���ꂽ�͂��̒l�v�͎̂Ă��܂�����A�����Ɍ덷�������܂��B���̂悤�ɁA�������̌v�Z�����炩���ߌ��߂��L�����őł��邱�Ƃɂ�萶����덷��ł���덷�Ƃ����܂��B
1-2-5�@10�i���̢7����1���2�i���\���������͎̂��̂����ǂꂩ�B�������A�����_�ȉ�16�ʂ܂ł�\�����Ă���B
(1)�@0.0101001000100001�@�@�@(2)�@0.0011011101111011
(3)�@0.0010010010010010�@�@�@(4)�@0.0001010000101000
(5)�@0.0111000000000000
������3
10�i�@�ł�2�i�@�ł����i�@�ł��A�����_�ȉ��́um�i�@�ɂ����鏬���_�ȉ�n���v��m-n�̌��ƂȂ�܂��B10�i�@�ł�0.1��10-1�ł����A2�i�@��0.1��2-1�ł��B���������āA���Ƃ��ΑI����(1)��0.0101001000100001�́A2-2+2-4+2-7+2-11+2-16�ƂȂ�܂��B
����܂��A�ȉ��ɉ����Ă݂܂��B
1/7��1/8+����2-3+���B2-3��2�i����0.001�Ȃ̂ŁA1/7��2�i����0.001+���B���̏����ɍ����I������(2)��(3)�B
�܂��i�肫��Ȃ��̂ŁA���ɂ��Č�������B
����1/�i7*8�j��1/56�B56��25�i32�j��26�i64�j�̒��ԂȂ̂�1/56��1/64+����2-6+���B
2-6��2�i����0.000001�Ȃ̂ŁA���2-3�ƍ��킹�A2�i����0.001001.���̏����ɍ����I������(3)�̂݁B�����(3)�������B
���ɂ����낢��ȉ�����������Ǝv���܂��B10�i�@��2�i�@�̊Ԃ̒��ōs�����藈����ł���ǂ�ȉ������ł������ɂ��ǂ蒅����Ǝv���܂��B
�y�ʉ�1�F�ÎZ�̂݁A�����@�z
1/7�̑O���1/2n��1/4�i��2-2�j��1/8�i2-3�j�ł���A1/7�͂��̊Ԃɂ���̂ŁA2-2��1/7��2-3��0.01��1/7��0.001�B
����Ă��̒i�K��(2)��(3)�ȊO�Ȃ��B(2)��(3)�̈Ⴂ��2-4�i��1/16�j��1���ǂ����B�܂�I����(2)��2-3+2-4���I����(3)�B
�܂�2-3+2-4��1/8+1/16��1.5/8�ł���A1.5/8��8/1.5��5.3�ł��邱�Ƃ���A1.5/8��1/5.3��1/7�B�����(2)���Ȃ��Ȃ�A�I����(3)���c��B
�y�ʉ�2�F�d��g�p�A�T�Z�z
�d��������Ă���ꍇ�i���邢��1/7���ÎZ�ł���ꍇ�j�A1/7��0.1428�������o��B
�@2-1��0.5
�@2-2��0.25
�@2-3��0.125
�@2-4��0.0625
�@2-5��0.03125
�@2-6��0.015625
�@�@�@�@�F
�@�@�@�@�F
�ł���A1/7�i0.1428�j��2-3�����傫���B�����0.1428-2-3��0.1428-0.125��0.0178
0.0178��2-6�����傫���B����� 0.0178��2-6��2�i����0.000001
�����1/7��2�i����2-3+2-6���x��0.001+0.000001���x��0.001001�@������ԋ߂��̂͑I����(3)
3�Q�@��͂Ɋւ�����́@(�S5��肩��3����I����)
1-3-1�@���}�̂悤�ɏ�[���Œ肳��A���[�ɉ������̉d���钆��~��������B���̉~���̉��[�̕ψʂ����e�l���������������̂ŁA������������������l����B���[�̕ψʂ��ł��������Ȃ�͎̂��̂����A�ǂ̏ꍇ���B�Ȃ��A�ޗ��̓t�b�N�̖@���ɂ��������e���̂ł���A�~���̒����͒��a�ɔ�r���ď\���傫�����̂Ƃ���B
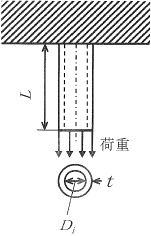
(1)�@�~���̒����k��2�{�ɂ���B
(2)�@�c�e���W���d�i�����O�W���j��2�{�̍ޗ����g�p����B
(3)�@�c�e���W���d��2����1�̍ޗ����g�p����B
(4)�@���a�c����ύX�����ɁA��������2�{�ɂ���B
(5)�@��������ύX�����ɁA���a�c����2�{�ɂ���B
������4
�ȉ��A�Վ��f����葺������̃��X�����p���܂��B
�@�@�~���̒����k���Q�{�ɂ���B
�@�@���̏ꍇ�A���́A�Ђ��݈��Œ������{�ɂȂ�̂ŕψʂ͔J�둝������ƍl�����܂��B
�A�@�c�e���W���d�i�����O�W���j���Q�{�̍ޗ����g�p����B
�@�@�Ё��d��
�@�@�㎮��艞�͈�艻�ł͂Ђ��݂͔����ƂȂ�A���������āA�ψʂ͔����i�~0.5�j�ƂȂ�܂��B
�B�@�c�e���W���d���Q���̂P�̍ޗ����g�p����B
�@�@�A�Ɠ��l�̍l��������ψʂ͂Q�{�ɂȂ�܂��B
�C�@���a�c����ύX�����ɁC���������Q�{�ɂ���B
�@�@�f�ʐς̎�������Ε�����܂��B�����A
�@�@A = �~t(D+2t)
�@�@�㎮���t���Q�{�ɂȂ��A���Q�{�ȏ�ɂȂ邱�Ƃ�������܂��B
�@�@���������ĉ��́A�Ђ��݂�1/2�����ƂȂ�܂��B
�D�@��������ύX�����ɁC���a�c�����Q�{�ɂ���B
�@�@�C�̎����AD���Q�{�ɂȂ��Ă�A�͂Q�{�ȉ��ł��邱�Ƃ�������܂��B
�@�@���������ĉ��́A�Ђ��݂�1/2�ȏ�ł��邱�Ƃ�������܂��B
���������āA�C�B
1-3-2�@�ޗ������`�e���̂ł��邱�Ƃ����肵���\�����̉��͕��L��L���v�f�@�ɂ���͂���Ƃ��̗v�f�����Ɋւ��鎟�̋L�q�̂����A�ł��s�K�Ȃ��̂�I�ׁB
(1)�@���͂̕ω����傫�������ɑ��ẮA�v�f�������ׂ�������ׂ��ł���B
(2)�@���͂̕ω��������������ɑ��ẮA���͎��̂̑召�ɂ�����炸�v�f�����̉e���͏������B
(3)�@�e���v�f�����ʼn�͂����ꍇ�ɂ͏�ɕό`�͏������Ȃ艞�͍͂��߂ɂȂ�̂ŁA���͕]���Ɋւ��Ă͈��S���ł���B
(4)�@�v�f�����̉e�������邽�߁A�ł���Ε����̗v�f�����ɂ���ĉ�͂��s���A���ʂ��r����̂��]�܂����B
(5)�@����d�ɑ��ėL��������F���ꂽ�v�f�����ł��A���̉d�ɑ��Ă͗L���Ƃ͌���Ȃ��B
������3
���b�V����e������Ɖ��͂��������Ȃ�A�댯���̕]���ƂȂ�܂��B
1-3-3�@���}�Ɏ����悤�ȗ��[�����̕ǂɌŒ肳�ꂽ�f�ʐςr�A�����^�̂͂肪����B�͂�������_���a�_�Ƃ��A�`�a�ԁA�a�b�Ԃ̏c�e���W���i�����O�W���j���d1�A�d2�Ƃ���Ƃ��A�d�o���͂�̎������ɕ��ׂ��ꂽ�ꍇ�̓_�a�̕ψʃƂ��Đ��������̂�(1)�`(5)�̒�����I�ׁB
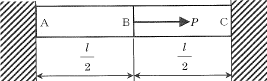
(1)Pl/2SE1�@�@(2)Pl/2SE2�@�@(3)Pl/2S(E1+E2)�@�@(4)3Pl/2S(2E1+E2)�@�@(5)Pl/2S(E1-E2)
������3
�ȉ��A�Վ��f����葺������̃��X�����p���܂��B
�B�ł��B
�l�����͈ȉ��̒ʂ�B
���Œ�P�ɔ���P1,P2���l���܂��B
���������̂肠�����A
P1+P-P2=0
P1-P2=-P (a)
�d��p�ʂł̕ψ�(�Ђ���)�͐�Βl�������B
�i���������k�A�����̈Ⴂ����j���Ȃ킿�A
��1=-��2 (b)
�܂��A
��1=P1/(S�EE1)
��2=P2/(S�EE2 (c)
(a)�A(b)�A(c)���
P1=-P�EE1/(E1+E2)
��1=-P/S(E1+E2)�@�@�@�i����/(L/2)�j
�����
��=PL/2S(E1+E2)
���Ȃ݂Ƀ}�C�i�X�͕���1�����k���ނƂ���P1�̌�����ݒ肵���̂ɑ��A���ۂ̕ψʂ͈��������ł��邱�Ƃ������܂��B
1-3-4�@���̐������ɂ���L���A�y�A�z�`�y�E�z�ɓ����ׂ����̂Ƃ��āA�K�ȑg������(1)�`(5)�̒�����I�ׁB�Ȃ��Aa1�Aa2�A����an(n��1�j�͔C�ӂ̐��̐����ł�����̂Ƃ���B
�@(1+a1)(1+a2)��������(1+an)
�@���y�A�z(1/2+a1/2)(1/2+a2/2)��������(1/2+a2/2)
�@���y�A�z(1+(a1-1)/2)(1+(a2-1)/2)��������(1+(an-1)/2)
�@�y�C�z�y�A�z(1+(a1-1)/2+(a2-1)/2)+��������+(an-1)/2)
�@�y�C�z�y�A�z(1+(a1-1)/(n+1)+(a2-1)/(n+1)+��������+(an-1)/n+1)
�@���y�A�z/�y�E�z(1+a1+a2+��������+an)
| �i�A�j | �i�C�j | �i�E�j | |
| (1) | 2�� | �� | n |
| (2) | 2n | �� | n |
| (3) | 2�� | �� | n |
| (4) | 2�� | �� | n�{1 |
| (5) | 2n | �� | n�{1 |
������4
1-3-5�@�C�̂̒舳�M�e�ʂƒ�ϔM�e�ʂ̔�́A�ʏ���ƕ\�������B��C�̃������߂邽�߂̎��̎����̐����ɂ��āA�m�@�A�@�n�`�m�@�E�@�n�ɓ������Ƃ��čł��K�ȑg������(1)�`(5)�̒�����I�ׁB
�@�}�̂悤�ɃK���X�r�ɃR���N�̐������A����ɒf�ʐς`�̃K���X�ǂ𐂒�������ɗ��Ă���A�K���X�ǂɃs�X�g���̖�ڂ����������������B�������A�K���X�ǂƋ������Ƃ̊Ԃɂ͌����������A���C�������ł�����̂Ɖ��肷��B
�@�����������t�ʒu����ړ������Ƃ����m�@�A�@�n����(����𐳂Ƃ���)�Ƃ���ƁA�������ɂ���ĕ����߂�ꂽ��C�̑̐ϑ������u�͎����ŕ\�����B
�@�@���u�����`
�@�܂��A���̂Ƃ��̓������͂̕ω������o�Ƃ���ƁA�������ɍ�p�����(����𐳂Ƃ���)�e��
�@�@�e���`���o
�ŗ^������B�����ŁA��C�����z�C�̂ł���A�������̕��t�ʒu����̂��ꂪ�\���������Ɖ��肷��ƁA�������ɂ���ĕ����߂�ꂽ��C�̕��t��Ԃł̑̐�av�u�ƈ���av�o��p����
�@�@���o����av�o���u/av�u
�̊W����������B�ȏ�̎���p����Ƃe�͈ȉ��̂悤�ɋ��܂�B
�@�@�e������av�o�`2/av�u
�{���́A�ψʂɔ�Ⴗ��J�ŋ��������m�@�C�@�n���Ƃ��Ӗ�����B���������āA���������m�@�E�@�n���A���̎����т͎����ŗ^������B
�@�@�с�2��(mav�u)/��(��av�o�`2)
�����ŁA���͋������̎��ʂł���B���̎���p����A�������̎����𑪒肷�邱�Ƃɂ���āA��C�̂������߂邱�Ƃ��ł���B
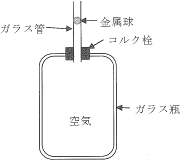
| �i�A�j | �i�C�j | �i�E�j | |
| (1) | ���t�ʒu����̂��� | �����߂���� | �P�U�� |
| (2) | �ʒu�G�l���M�[�̑��� | ����������� | �����^�� |
| (3) | ���t�ʒu����̂��� | �����߂���� | �����^�� |
| (4) | �ʒu�G�l���M�[�̑��� | �����߂���� | �����^�� |
| (5) | ���t�ʒu����̂��� | ����������� | �P�U�� |
������1
�ȉ��A�Վ��f���ӂ�������̃��X�����p���܂��B
��蕶�͒����ł����A�|�C���g�����ǂ߂��ޖ�肾���������E�E�E
�����Ɨ��Ă��鎞�_�ŒP�U���B
�U��������A�͂Ƃ��Ắu�����߂����v�B
�u�{���́C�ψʂɔ�Ⴗ��J�ŁE�E�E�v�Ƃ��邩�炙�͕ψʁ�����B
����ć@�B
4�Q�@�ޗ��E���w�E�o�C�I�Ɋւ�����́@�i�S5��肩��3����I���j
1-4-1�@���̃A�`�I�̔Z�x�̊e���n�t1�k�i���b�g���j�����A(1)�`(5)�̑g�����ō�������Ƃ��A�����鐅�n�t���_���ɂȂ���̂�I�ׁB
�A�@1.0 mol/L�@���_�iH2S04�j
�C�@2.0 mol/L�@���_���i�g���E���iNaOH)
�E�@1.0 mol/L�@���_�iHCl�j
�G�@2.0 mol/L�@�A�����j�A���iNH4OH�j
�I�@1.0 mol/L�@�|�_�iCH3COOH�j
(1)�@�A�ƃC�@�@�@�@(2)�@�A�ƃG�@�@�@�@(3)�@�C�ƃE�@�@�@�@(4)�@�C�ƃI�@�@�@(5)�G�ƃI
������2
�_�̓A�A�E�A�I�ł����A�A�̂��_�ŁA�S��1mol�B����Đ�����(1)��(2)�ɂȂ�܂��B
���_���i�g���E���͑S�ĉ𗣂��鋭����ł���A2H+2OH��2H2O�B�܂蒆���B
����A�����j�A���͑S�ĉ𗣂����㉖��ƂȂ�A���_�ƍ�������Ǝ�_���ɂȂ�܂��B
1-4-2�@���~�d�r�̔����Ɋւ��鎟�̕��͂́m�@�A�@�n�`�m�@�I�@�n�ɓ�����̑g�����Ƃ��āA�ł��K�Ȃ��̂�(1)�`(5)�̒�����I�ׁB
�@���~�d�r�͊_�ɉ��̓d�ɂƓ�_�����̓d�ɂ�Z�����d�r�ł���A�N�d�͖͂�2�u�ł���B���d�ɂƂ��Ȃ��m�@�A�@�n�ɂ����āi���j�̔������A�m�@�C�@�n�ɂ����āi���j�̔�����������B
�@�@�@Pb�{SO42-�@���@PbSO4�{2e-�@�@�@�@�@�@�@�@�@ �@�ia�j
�@�@�@PbO2�{4H+�{SO42-�{2e-�@���@PbSO4�{2H2O�@�@�@�@�ib�j
�@���d�����ł́A�m�@�E�@�n���_������A�m�@�G�@�n���Ҍ������B�܂��A���d�ɂ�藰�_�����_���ɂȂ�ƂƂ��ɁA�_�̖��x���m�@�I�@�n�Ȃ�B
| �i�A�j | �i�C�j | �i�E�j | �i�G�j | �i�I�j | |
| (1) | ���� | ���� | �� | �_���� | �傫�� |
| (2) | ���� | ���� | �_���� | �� | �傫�� |
| (3) | ���� | ���� | �_���� | �� | ������ |
| (4) | ���� | ���� | �_���� | ���_�� | �傫�� |
| (5) | ���� | ���� | �� | �_���� | ������ |
������5
�d�r�ł͕��ɂ���d�q�����ɂɗ���܂��B(a)�̔����ł͓d�q���������A(b)�ł͓d�q������Ă��܂�����A�i�A�j�͕��ɁA�i�C�j�͐��ɂł��B�i�́A���w�Z�̗��Ȃ̎��ƂŌ���NHK����e���r������ł悭����Ă��܂����j
���Ɏ_���ƊҌ��ł����A�d�q���������Ƃ��_���A��邱�Ƃ��Ҍ��Ƃ����܂�����A�i�E�j�͉��A�i�G�j�͎_�����ł��B����Ő�����(1)��(5)�ɍi���܂����B
�����ė��_�����_���ɂȂ��Ă����̂ł����痰�_�͌����Ă����܂��B����āi�I�j�́u�������v�B
�S�̂ɍ��Z���w���x�̃��x���ŏ\�������܂��B
�������ł͉���̂��߂Ɂi�A�j���珇�ɍl���čs���܂������A���ۂ̎����ł͂킩��Ƃ��납��i�荞��ł����܂��B���Ƃ��i�I�j�Ȃǂ͒����Łu�������v�ł��邱�Ƃ��킩��܂�����A�ŏ����琳����(3)��(5)�ɍi�荞�܂�܂��B(3)��(5)�̈Ⴂ�́i�E�j�Ɓi�G�j�ł�����A�i�A�j��i�C�j�ɂ͖ڂ����ꂸ�Ɏ_���Ҍ��̂��Ƃ��l����A�v���ɐ������i�荞�߂܂��B
1-4-3�@������ޗ��̐����ɊJ���鎟�̋L�q�̂����A�ł��s�K�Ȃ��̂�I�ׁB
(1)�@�V���J�Q���⊈���Y�ɂ͔��ׂȋ����������āA�P�ʎ��ʂɑ���\�ʐς�����߂đ傫���A�z���܂Ƃ��ĒE�L�E�E�F�ȂǂɎg����B
(2)�@�V�R�K�X�̎听���̓x���[���ł���A��p���k���ĉt�̂ɂ������̂��t���V�R�K�XLNG�Ƃ����B LNG�͓s�s�K�X�p�≻�w�H�Ƃ̌��ޗ��ȂǂɎg����B
(3)�@���͐ԐF����̂�������ŁA�d�C�E�n�̗Ǔ��̂ł���B����������C���ł͏퉷�ŕω����ɂ������A���C�̂����C���ł͎_������ėΐ���B
(4)�@�_���`�^���Ɏ��O����������ƁA�����w�������N�����A���̂Ƃ������銈���_�f�͂��܂��܂ȗL�@�������A�R�ۂ�E�L�A����h�~�Ȃǂ̌��ʂ������炷�B
(5)�@�X�e�����X�|�ɂ̓N�������܂܂�Ă���A�\�ʂɃN�����̎_���疌���ł��A���ꂪ�s���ԂƂȂ邽�ߗD�ꂽ�ϐH���������B
������2
(1)�������@�V���J�Q���͊����܂Ƃ��Ă��悭�ڂɂ��܂����A�E�L�E�E�F���ʂ�����A�L���Ƃ��Ă悭�p�����Ă��܂��B
(2)�����~�@�x���[���ł͂Ȃ����^���ł��B�x���[���͏퉷�ł��łɉt�̂ł�����A�K�X�R���ɂ͎g���܂���B
(3)�������@�K��_�ЂȂǂœ��ŕ��̉����͂��������F�����Ă��܂��ˁB������u�ΐv�i�낭���傤�j�Ƃ����܂��B
(4)�������@�_���`�^���̃R�[�e�B���O���́A���O�����z������ƕ\�ʂŌ��G�}�����ɂ��C�I�����_�f���q�����A�L�@�������_���������܂��B
(5)�������@�X�e�����X���߂�����h�������Ȃ��Ă��K�тȂ��̂́A�܂��ɂ��̃N�����̎_���疌���ł��邽�߂ł��B
1-4-4�@�A�������̑̂�����A�܂��̓��̉��w�������o�����X�悭�i�߂邽�߂ɂ́A��ʂɏ��Ȃ��Ƃ�16��ނ̌��f�i�Y�f�A�_�f�A���f�A���f�A�����A�J���E���A�J���V�E���A�}�O�l�V�E���A�C�I�E�A�S�A�}���K���A�z�E�f�A�����A�����u�f���A���A���f�j���K�v�Ƃ���Ă���B���ʂł��ꂼ�ꊣ���A���̂̂ق�0.1���ȏ���߂�9���f�𑽗ʌ��f�ƌĂсA����ȉ���7���f����ʌ��f�Ƃ����B����猳�f�ɂ��āA�A���Ɣ엿�Ɋւ��鎟�̋L�q�̂����A�ł��s�K�Ȃ��̂�I�ׁB
(1)�@16���f�̂����Y�f�A�_�f�A���f�́A�������̌����ɂȂ��_���Y�f�Ɛ������荞�܂��̂ŁA�⋋�̕K�v�͂Ȃ��B
(2)�@�엿�Ƃ́A�_�앨�̎��ʂ𑝂₵����A�����ɕs���������Ȍ��f��A���ɕ⋋���邽�߂ɗ^���镨���ł���B
(3)�@�V�R�엿���{���ƁA�܂܂�Ă���L�@���̎_�������ɂ���ē�_���Y�f���邪�A�y����_���������邱�Ƃ͂Ȃ��B
(4)�@���w�엿�ɂ́A���f�A�����A�J���E���̂ǂꂩ���听���Ƃ������@�������������B
(5)�@���ʌ��f�́A�A���̓��̍y�f�̐����Ƃ��Ċ܂܂����̂�A�y�f�̊������A�������ȂǂɕK�{�Ȃ��̂������B
������3
(1)�������@���̂Ƃ���B
(2)�������@���̂Ƃ���B���ꂪ�엿�̊�{�I�l�����ł��B
(3)�����~�@��_���Y�f�𐅂ɗn�����Ǝ_���ɂȂ�܂��B�n�����g���̈�̖��Ƃ��ĊC�m�_�������w�E����Ă��܂��B
(4)�������@���̂Ƃ���B
(5)�������@���̂Ƃ���B
1-4-5�@��`�q����ɊJ���鎟�̕��͂́m�@�A�@�n�`�m�@�G�@�n�ɓ�����̑g�����Ƃ��āA�A�Ȃ��̂�(1)�`(5)�̒�����I�ׁB
�@�^���̂ƂȂ�DNA�A���Ȃ킿�m�@�A�@�n�ɍy�f�Ȃǂ�p���Ĉَ��DNA�������Ǔ��őg�ݍ��݁A������h���זE���ɓ������邱�Ƃ�g����DNA�����Ƃ����A�܂��A���̂悤�ɂ��ē���ꂽDNA��g������DNA�ƌĂԁB�����̑g�����̂̒����瓯��̈�`��������DNA��P�����邱�Ƃ��m�@�C�@�n�Ƃ����B��`�q�g�����ɗp������y�f�ɂ́ADNA���������邽�߂�DNA�|�������[�[,�ARNA�𒒌^�Ƃ���DNA����������t�]�ʍy�f�ADNA�����̉���z��̕����Őؒf�����X���m�@�E�@�n�ADNA�̒f�Ђ�A������DNA�m�@�G�@�n�Ȃǂ�����B
| �i�A�j | �i�C�j | �i�E�j | �i�G�j | |
| (1) | �x�N�^�[ | �N���[�j���O | �����y�f | ���K�[�[ |
| (2) | �x�N�^�[ | �X�N���[�j���O | �����y�f | ���p�[�[ |
| (3) | �x�N�^�[ | �N���[�j���O | �����y�f | ���K�[�[ |
| (4) | �v���[�u | �X�N���[�j���O | �����y�f | ���K�[�[ |
| (5) | �v���[�u | �N���[�j���O | �����y�f | ���p�[�[ |
������1
�ȉ��A�Վ��f����肿��[�͂�̃��X�����p���܂��B
�@�ł��BDNA�̉^�щ��̓x�N�^�[�ADNA�ؒf�͐����y�f�ADNA�A���̓��K�[�[�ł��B
5�Q�@�Z�p�A�ց@�i�S5��肩��3����I���j
1-5-1�@�d�C�G�l���M�[�̒����┭�d�ɊԂ��鎟�̋L�q�̂����A���������ł��s�K�Ȃ��̂�I�ׁB
(1)�@�V�R�K�X�������d�ł́A�V�R�K�X�̔R�ăK�X�̃G�l���M�[�𗘗p���Ă܂����C�^�[�r��������A���̔r�M��p���ăK�X�^�[�r�����쓮�������Ƃɂ��A�����I�Ȕ��d�������グ�Ă���B
(2)�@�ꎟ�d�r�Ƃ́A�}���K�����d�r�̂悤�Ɉ�x�Ŏg������ƂȂ�A�Ăюg�p�ł��Ȃ��d�r�̂��Ƃł���A�d�r�Ƃ́A���`�E���C�I���d�r��Ni-Cd�d�r�̂悤�ɁA�[�d���čĂюg�p���邱�Ƃ̂ł���d�r�̂��Ƃ������B
(3)�@�d�C��d�w�L���p�V�^�͋}���ȏ[���d���\�ł���A�[���d�T�C�N���������D�ꂽ�~�d�f�o�C�X�ł���B�ߔN�A�n�C�u���b�h�����Ԃ�R���d�r�ԂŃG�l���M�[�̗L�����p��ړI�Ƃ����d�C��d�w�L���p�V�^�̓��ڂ���������Ă���B
(4)�@�g�����d�́A��Ԃ̗]��d�͂Œ����r�Ȃǂɂ���Ꮚ�̐��������ɂ��ݏグ�A���̈ʒu�G�l���M�[�𗘗p���Ē��Ԃɔ��d�������̂ł���A�d�C�G�l���M�[������V�X�e���Ƃ�����B
(5)�@�R���d�r�́A�u���̓d�C�����v�Ƌt�̌����Ŕ��d����B���̓d�C�����́A���ɊO������d�C��ʂ��Đ��f�Ǝ_�f�ɕ������邪�A�����̔R���d�r�́A���f�Ǝ_�f��d�C���w���������ēd�C�����B
������1
�K�X�̃G�l���M�[�𗘗p����̂��K�X�^�[�r���A�r�M���g���̂����C�^�[�r���ł��B
1-5-2�@�킪���̎�����T�C�N���Ɋւ��鎟�́i�A�j�`�i�G�j�̋L�q�ɂ��āA����̑g�����Ƃ��čł��K�Ȃ��̂�(1)�`(5)�̒�����I�ׁB
�i�A�j�Ζ��Ȃǂ̉��ΔR���̎������͒Ⴂ�{�����z�������͖L�x�ł���A�Ƃ��ɍ|�z�̎������͌��݂ł�50���ȏ�i���̊ܕ��Ƃ��Čv�Z�j�ł���B
�i�C�jPET�i�|���G�`�����e���t�^���[�g�j�{�g���͏ċp����ƃ_�C�I�L�V������ʂɐ������邱�Ƃ��m���Ă��邽�߁A���ʉ���A��čĎg�p���邱�Ƃ��i�߂��A���̊����͉���ʂ�20�����Ă���B
�i�E�j�g�p�ς݂̈����p�A���~�j�E���ʂ́A80���ȏオ�������A���̉ߔ����A���~�j�E���ʂ̌����Ƃ��ė��p����Ă���B�܂��A��������g�p�ς݃A���~�j�E���ʂ�Z�����čĐ��n����ق����A�z�B���ĐV�n��������A���ʂ̃A���~�j�E��������̃G�l���M�[������Ȃ��Ă��ށB
�i�G�j�����Ԃ̔r�o�K�X�̂��߂̐G���X�R���d�r�ɗp�����锒���́A���̕����ナ�T�C�N�����邱�Ƃ�����ł��邪�A���ɔ�ׂĎ��������ʂ��i�i�ɖL�x�ň����ł���A���ۑS��Z�p�̃R�X�g�ጸ�̂��߂ɑ�ʂɗ��p����Ă���B
| �A | �C | �E | �G | |
| (1) | �� | �� | �� | �� |
| (2) | �� | �� | �� | �� |
| (3) | �� | �� | �� | �� |
| (4) | �� | �� | �� | �� |
| (5) | �� | �� | �� | �� |
������2
�A�����~�@���̎�������0%�ł��B
�C�����~�@PET�ɂ͉��f�͊܂܂�܂���̂ŁA�R�₵�Ă��_�C�I�L�V���͏o�܂���B�܂��������60%���Ă��܂��B
�E�������@�L�q�̒ʂ�ł��B
�G�����~�@�����͊����ł��B�ȏ�ɂ�萳����(2)�ł��B�~�ɂȂ��Ă�����̂́A����������o�I�ɉ��������Ƃ��킩��̂ł͂Ȃ����Ǝv���܂��B
1-5-3�@ppm�i�s�[�E�s�[�E�G���j�Ƃ́Aparts per million�̗��ŁA�����̕����̔Z�x��\������ۂɂ悭�p������P�ʂł���A���ʔ�A�̐ϔ�̂�����ɂ��K�p�����B���́i�A�j�A�i�C�j�ŏq�ׂ�2�̔Z�xa�Ab�̊W�̂����A�K�Ȃ��̂�(1)�`(5)�̒�����I�ׁB
�i�A�j�[��1���A����20m�A��10m�̃v�[���ɖ������ꂽ�����ɁA1kg�̐H�����ψ�ɗn�������Ƃ��ɂł���H�����̔Z�x��a�ippm�j�Ƃ���B�������A�Z�x�͎��ʔ�Ƃ���B
�i�C�j�c6���A��5���A����4���̖����ꂽ1�C���̕����̒��ŁA1���b�g���A1.2�C���̃w���E���̓��������D���j�A�w���E���������̋�C�Ƌψ�ɍ��������Ƃ��̕����̋�C���̃w���E���Z�x��b�ippm�j�Ƃ���B�������A�Z�x�͑̐ϔ�Ƃ��A��C���ɂ͕��D�̔j���O��5
ppm�̃w���E�����܂܂�Ă������̂Ƃ���B
(1) a��2b�@�@�@�@(2) a��b�@�@�@�@(3) a��b��2a�@�@�@�@(4) 2a��b��5a�@�@�@�@(5) 10a��b
������4
(�A)�@�v�[���̐���1�~20�~10��200m2�B���̖��x��1�Ȃ̂�200����200,000kg�B�����1kg�Ȃ̂ŁA1��200,000��5�~10-6��5ppm�B
�@�@�@�Ȃ��Appm�́uper million�v�Ƃ���ʂ�A�S�������A10-6�ł��B
(�C)�@�����̋�C��6�~5�~4��120m3��120,000L�B������1L�A1.2�C���̃w���E�������o�����̂ŁA�w���E����1�~1.2��1.2L�B
�@�@�@����āA1.2��120,000��1�~10-5��10ppm�B���Ƃ���5ppm�Ȃ̂ŁA���v15ppm�B
����āAa��b��(1)�A(2)�͊Y�������A2a��10ppm��b��菬�����̂�(3)���s�����B(4)��10��15��25�Ő����B(5)��10a��50�ɂĕs�����B
1-5-4�@�ۑS�ɊԂ��鎟�̕��͂́m�@�A�@�n�`�m�@�I�@�n�ɓ�����̑g�����Ƃ��āA�K�Ȃ��̂�(1)�`(5)�̒�����I�ׁB
�@�ݔ���@�B�Ȃǂ̑Ώ�(�ȉ��A�A�C�e���ƋL��)���^�p�\��Ԃňێ����A�̏�Ȃǂ����邽�߂̏��u�y�ъ����́A�ۑS�ƌĂ��B�ۑS�́A�A�C�e�����g�p���Ɍ̏Ⴗ�邱�Ƃ𖢑R�ɖh�~���邽�߂ɁA�K��̊Ԋu���ɏ]���ăA�C�e���̋@�\��̏�̊m����ጸ����Ƃ����m�@�A�@�n�ۑS�ƁA�t�H�[���g�̔�����ɃA�C�e����v���@�\���s��ԂɏC�������m�@�C�@�n�ۑS�Ƃɑ�ʂ����B�܂��A�m�@�A�@�n�ۑS�́A��߂�ꂽ���Ԍv��ɏ]���čs�����Ԍv��ۑS�ƁA�A�C�e���̓����ԁX�X���̃��j�^�����O�Ɋ�Â��čs���m�@�E�@�n�ۑS�Ƃɕ�������B�@����ɁA���Ԍv��ۑS�́A�\��̎��ԊԊu�ōs���m�@�G�@�n�ۑS�ƁA�A�C�e�����\��̗ݐϓ��쎞�Ԃɓr�����Ƃ��ɍs���m�@�I�@�n�ۑS�Ƃɕ�������B
| �i�A�j | �i�C�j | �i�E�j | �i�G�j | �i�I�j | |
| (1) | ��� | ���� | ���� | ��ԊĎ� | �\�h |
| (2) | ��ԊĎ� | ���� | �\�h | ��� | ���� |
| (3) | ��� | �o�� | �\�h | ��ԊĎ� | ���� |
| (4) | �\�h | ���� | ��ԊĎ� | ��� | �o�� |
| (5) | �\�h | ��� | ��ԊĎ� | ���� | ���� |
������4
��ʓI�ɐݔ��ۑS�̑̌n�͈ȉ��̂悤�ɂȂ��Ă��܂��B�i�u�Z�p�m���x�ɂ����鑍���Z�p�ė�����̋Z�p�̌n�v�Q�Ɓj
| 1.�\�h�ۑS | A)����ۑS �@����I�ȗh�~�E����E�������� |
| B)����ۑS �@����_���ƃI�[�o�[�z�[�� |
|
| C)�\�m�ۑS �@�X�����Ǘ����ۑS�����E���������߂� |
|
| 2.���ǕۑS �@�̏Ⴕ�Ȃ��悤�A���P�������ݔ���̎�_��⋭ |
|
| 3.����ۑS �@�̏��~�E�L�Q�Ȑ��\�ቺ���������Ă���C�� |
|
| 4.�ۑS�\�h �@�ݔ��X�V�i�K�ŁA�M�����E�o�ϐ��Ȃǂ�������ۑS��E���������Ȃ����� |
|
�I�����̋L�ړ��e�Ƃ͈قȂ�܂����A��g�ɂ��Ă̋L�q�ł���i�A�j�Ɓi�C�j�ɓ���Ƃ���A�u�\�h�v�Ɓu����v�ł��邱�Ƃ͂킩��܂��B���̎��_��(4)�����Y�����Ȃ��킯�ł����A���Ƃ͊��o�I�ɑÓ��Ȍ��t���I�ׂ�Ǝv���܂��B
����āA������(4)�ł��B
1-5-5�@�m�I���Y��{�@�i����15�N7�������j�Ɋւ��鎟�̋L�q�̂����A�ł��s�K�Ȃ��̂�I�ׁB
(1)�@���̖@���́A�m�I���Y�̑n���A�ی�y�ъ��p�Ɋւ��A��{���O�y�т��̎�����}�邽�߂Ɋ�{�ƂȂ鎖�����߂����̂ł���B
(2)�@���̖@���ŁA�m�I���Y�Ƃ́A�����A�l�āA�����̐V�i��A�ӏ��A���앨���̑��̐l�Ԃ̑n���I�����ɂ�萶�ݏo�������́A���W�A�����Ȃǂ̏��������B
(3)�@���̖@���Œm�I���Y���Ƃ́A�������A���p�V�Č��A�琬�O�A�ӏ����A���쌠�A���W�����̑��̒m�I���Y�Ɋւ��Ė@�߂ɂ���߂�ꂽ�������͖@����ی삳��闘�v�ɌW�錠���������B
(4)�@���́A�m�I���Y�̑n���A�ی�y�ъ��p�Ɋւ����{���O�ɂ̂��Ƃ�A�m�I���Y�̑n���A�ی�y�ъ��p�Ɋւ���{������肵�A�y�ю��{����Ӗ���L����B
(5)�@�m�I���Y�̑n���A�ی�y�ъ��p�Ɋւ���{��̐��i�́A�n�����̂��錤���y�ъJ���̐��ʂ̋��L����}��A���E�̎Y�Ƃ̎����I���W�Ɋ�^������̂ƂȂ邱�Ƃ��|�Ƃ��āA�s���Ȃ���Ȃ�Ȃ��B
������5
(1)�͒m�I���Y��{�@��1���̖ړI�̂Ƃ���ł��B
(2)��(3)�͖@��2���̒�`�̂Ƃ���ł��B
(4)�͖@��5���̂Ƃ���ł��B
(5)�́A�u���E�̎Y�Ɓv�ł͂Ȃ��A�u�䂪���Y�Ɓv�̎����I���W�Ɋ�^����ƂȂ��Ă��܂��B
����āA������(5)�ł��B