技術士第一次試験 平成17年度 基礎科目
問題・正解・解説
第一次試験過去問題Topへ
※技術士会公表の正解について、臨時掲示板での情報から解説を作成しました。
異論や情報などありましたら、メールにてお願いします。
*:出題ミスにより全員正解
1群 設計・計画に問するもの (全6問題から3問題を選択解答)
1-1-1 下図は、システム信頼性解析の一つであるFTA(Fault Tree Analysis)図である。図で、記号(a)は、その下流(下側)の事象が同時に生じた場合に、上流(上側)の事象が発現することを、記号(b)は、下流の事象のいずれかが起きた場合に上流の事象が発現することを意味する。事象Aが発現する確率に最も近い値を選べ。最下段の枠内の数値は、最も下で起きる事象の発現確率を表す。なお、記号の下流側の事象の発生はそれぞれ独立事象とする。
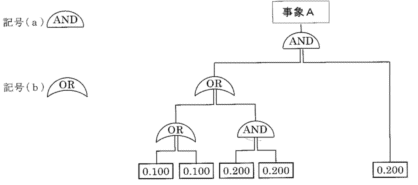
(1) 0.200 (2) 0.044 (3) 0.048 (4) 0.203 (5) 0.204
正解は2
左下:0.1 OR 0.1→1-(1-0.1)*(1-0.1)=1-0.9*0.9=1-0.81=0.19
その右:0.2 AND 0.2→0.2*0.2=0.04
よって2段目は0.19 OR 0.04→1-(1-0.19)*(1-0.04)=1-0.81*0.96=0.2224
3段目は0.222 AND 0.2→0.222*0.2=0.0444
よって2。
●AND条件(直列)は掛け合わせる・・・・A AND B → A*B
●OR条件(並列)は1から除したものを掛け合わせて最後に1から除する・・・・A OR B → 1-(1-A)*(1-B)
ということを覚えていれば、難なく解けます。
戻る
1-1-2 凸部と凹部(例えば、軸と穴)が組み合う場合、組み合う部分の幅寸法の分布が次式で表される正規分布に近似できる。
凸部の幅(例えば、軸の外径):N(μ1,σ12)
凹部の幅(例えば、穴の内径):N(μ2,σ22)
ここで、μiは平均値、σiは標準偏差である。(i = 1、2)
この2つの部品を組み合わせた場合に生じるすき間寸法の分布を表すものを選べ。ただし、すき間がある場合はすき間寸法は正であるとする。
(1) (μ,σ2)={(μ1+μ2)/2,(σ12+σ22)/2}
(2) (μ,σ2)={(μ1+μ2),(σ12+σ22)1/2}
(3) (μ,σ2)=(μ1/μ2,σ12/σ22)
(4) (μ,σ2)={(μ2-μ1),(σ12+σ22)1/2}
(5) (μ,σ2)={(μ1-μ2),(σ12+σ22)1/2}
正解はなし(出題ミスにより、全員正解)
おそらく(4)を正解としようとしたのでしょうが、分散が(σ12+σ22)1/2ではなく、(σ12+σ22)でないといけません。
以下、仮に(4)がちゃんと (4) (μ,σ2)={(μ2-μ1),(σ12+σ22)}になっていた場合について、正解を絞り込む過程を考えてみます。
最低条件として、正規分布がN(平均値,標準偏差の2乗=分散)であることを知らないと始まりません。これは高校数学レベルですが、標準偏差や最小二乗法、相関係数などとともに、科学技術に携わる者であれば最低限知っておかねばならないものでしょう。
さて、とすれば、軸の外径や穴の内径の平均値はμです。そして、「すき間」は、μ2が穴の内径、μ1が軸の外径ですから、この差であることは感覚的にわかります。すき間は軸が穴に対して細いときに生じます。つまり、μ2>μ1であり、そのすき間の寸法は、μ2-μ1です。
この時点で、正解は(4)しかありえません。分散がどうのこうのと考えずとも、正解選択肢は絞り込めます。引き算としては(5)もありますが、すき間寸法は正であると書いてありますので、これは正解選択肢ではありえません。
これでこの問題を解く作業は終わりです。択一問題は、正解がわかればそれでいいのですから、分散のことについて考える必要はありません。
結果的には分散の部分にミスがあって正解がなくなりましたが、1点稼いだことには変わりありません。つまり、やはり分散について考える必要はなかったわけです。
戻る
1-1-3 JIS Z 8311:1998 「製図−製図用紙のサイズ及び図面の様式」で規定されている、図面として具備しなければならないもののみを挙げているものを選べ。
(1) 中心マーク、輪郭線、方向マーク
(2) とじ代、中心マーク、輪郭線
(3) 中心マーク、輪郭線
(4) とじ代、輪郭線、方向マーク
(5) 輪郭線、方向マーク
正解は3
JIS Z 8311の第2章には、「輪郭」、「中心マーク」、「方向マーク」等々の説明があり、「輪郭」、「中心マーク」については「・・・ねばならない」と表現されていますが、「方向マーク」は「・・・2個の方向マークを設けてもよい」とあり、「具備しなければならない」とはいえません。
よって、具備しなければならないのは、中心マークと輪郭線。方向マークは必ずしも具備せずともよいので、正解は3。
出題意図がよくわかりません。これは修習技術者が備えねばならない知識なのか?という疑問があります。良問とはいえないと思います。
戻る
1-1-4 次の記述の(ア)〜(オ)には、A : De facto standard (事実上の標準)とB : De jure standard (正当な、法律上の標準)のいずれかが入る。その組合せとして最も適切なものを選べ。
情報通信分野をはじめとする多くの工業分野では、市場でのシェアの優位性を背景に(ア)が形成されることが多い。一方、各分野で国際標準を策定する場合には、安全性や信頼性などの要件の統一を考慮して(イ)としての性格をもつ標準が作られることが少なくない。国あるいは地域ごとに異なった(ウ)がすでに形成されている場合、その聞の競争の側面もあり、国際標準策定過程の投票権を有する同数のシェアと製品の流通シェアが一致しないことが、問題を引き起こすこともある。公共調達にかかねるWTO/TBT協定上、我が国も国際標準の尊重が求められているが、例えばセメント材料や地盤分類などをはじめとする粉体の、分級のフルイの目にかがある我が国の(エ)と国際標準との不整合が、近年危機感をもって受け止められたことは記憶に新しい。一方、(オ)の概念は製造物資仕法の責任範囲とも関係しており、製品の安全性・信頼性に関するstate of the artsを常に認識しておく必要がある。
|
(ア) |
(イ) |
(ウ) |
(エ) |
(オ) |
| (1) |
A |
B |
A |
A |
A |
| (2) |
A |
B |
A |
A |
B |
| (3) |
A |
B |
B |
B |
A |
| (4) |
A |
B |
B |
B |
B |
| (5) |
A |
B |
B |
A |
B |
正解は2
(ア)は明らかにデファクトスタンダード、(イ)は明らかにデジュールスタンダードです(デファクトに対峙するものとして記述されている)。
(ウ)と(エ)はどちらともつかないので、(オ)に注目すると、state of the artsは、「この値にしなさい」というものではなく、「その基準をクリアしていれば、あとは市場競争の中で決めていこうじゃないか(品質勝負でいこうじゃないか)」という考え方であり、これをミニマム・リクワイアメントとして、デファクトを作っていくものです。よって、(オ)はB。これで正解は(2)、(4)、(5)のどれかということになります。
(ウ)の事例として(エ)が上げられているので、(ウ)と(エ)は同じ。よって(5)は不正解。
「国あるいは地域ごとに異なった(ウ)がすでに形成されている」とあるが、デジュールスタンダードは「形成する」ものではなく「決めておく」ものであり、「正当な、法律上の標準」の概念にも文章は合わないので、(ウ)はデファクトと思われます。この時点で、選択肢(4)も誤りなので、正解は(2)。
結局のところ、デジュールスタンダードというものをどう解釈するかがポイントです。
ここで、ふるいの目はAかBか、すなわちJISはデファクトスタンダードか?デジュールスタンダードか?ということについて少し考えてみます。
例えばこちらを見るとJISはデジュールスタンダードの例として示されています。また、こちらを見ると、デファクトスタンダードであるVHSがJIS認定されているということが書かれていますが、これを「だからJISはデファクト」と解釈するか、「デファクトがデジュールになった例」と解釈するかは、意見の分かれるところではないでしょうか。
結局、デファクトとデジュールの境界というのは、結構ファジーな部分があるということかと思います。「デファクトはどこまで行ってもデファクト」であれば、それを追認した規格はデジュールになりえませんし、規格による追認でデジュールに「昇格」するのであれば、じゃあどの規格ならデジュールといえるのか、社内規格から地域規格、学会基準、JIS、ISO....と境界がファジーです。
ということで、そういったファジーな部分を含んでいる問題ゆえに適切でない、ともいえるでしょう。
一方、もし(ウ)がAしかあり得ないのであれば、「ABA*B」となって、正解は(2)しかなくなります。仮に(エ)をBと考えたとしても「ABABB」という選択肢がない以上、(2)しかないだろう、という論法もわからなくはありません。
ただ、じゃあ「ABAAB」が正しいのか、というと、「そうとは限らない」(意見が分かれる)ということで、「ABAABは間違いとは言えない」という、非常に消極的な根拠による正解選択肢ということになるのかなと思います。
したがって、出題ミス(間違い)と断定はできないけれど、それに近い、非常に不適切な問題である、というのが私の結論です。
戻る
1-1-5 プロジェクトの代替案としてA、B、C、D、E、Fがあり、これらの間に比較優位の順位付けが求められている。しかし、判定の困難さから、2個一組の一対比較でしか優劣がつけられないものとする。これまでの調査で、B>A、D>C、E>F、E>B、B>C、D>Eであることが判明した。これによって得られる判断として正しいものを選べ。ただし、これらの案の間には明確な順位付けが可能で、調査によって得られた優劣判断には誤りがないものとする。
(1) まだ「6案中○位」という順位付けのはっきりしている案はない。
(2) 「6案中○位」という順位付けのはっきりしている案は1個だけある。
(3) うまく組合せを選べば、あと2回の比較で必ずすべての順位付けを確定できる。
(4) うまく組合せを選んでも、あと2回の比較ですべての順位付けが確定できる確率は50%である。
(5) どのように組合せを選んでも、あと2回の比較ではすべての順位付けが確定できる可能性はない。
正解は4
文章から確定するのは、以下の事項です。
a) D>E>B>Aである。
b) Dが一番大きいということは確定している。
c) Eが2位であることも確定している。
d) FはEより小さいということ以外はわからない。したがって、Fは3位以下である。
e) CはBより小さく、Dより小さい。D>Bだから、CはAの前後の順位である。F>Cであれば、Cは5位か6位、F<Cであれば、Cは4位か5位である。
以上より、まずb)とc)から、(1)と(2)は除外されます。
ここで、
FがBより上か下かを判定しないと、全順位が確定しない。
同様に、CとAも比較せねばならない。
ということで、最低でも2回の比較が必要です。
FとB、CとAを比較したとき、
F>B & A>C → D→E→F→B→A→C で確定
F>B & C>A → D→E→F→B→C→A で確定
B>F & A>C → F、A、Cの順位が未確定
B>F & C>A → F、C、Aの順位が未確定
となり、順位が確定する可能性は2/4=50%ですから、正解は(4)。
4通りの比較結果を全て考えなくても、確定することがあり得るということがわかれば(5)は消えますし、逆に確定しなかった場合を想定できれば(3)は消えます。つまり、選択肢(4)は、「あと2回の比較ですべての順位付けが確定できるとは限らない」というように読み替えてもいっこうにかまわないわけです。「50%」という数字に惑わされないこと(50%だろうか、25%などではないだろうか、などと考えないこと)がポイントです。
戻る
1-1-6 単位期間中の故障発生確率が1%であるように調整されたシステムがある。このシステムを100単位期間稼動させたとき、この期間内に故障がまったく発生しない確率は次のうちどれに最も近いか。ただし個々の単位期間における故障の発生は、それぞれ独立事象とする。
(1) ほぼO (2) 約1/3 (3) 約1/2 (4) 約2/3 (5) ほぼ1
正解は2
故障発生確率が1%ということは、故障が発生しない確率は99%。
これが100回繰り返して成立する確率なので、0.99の直列(AND条件)。
よって、0.99100=0.366≒1/3。(あるいは(1-0.01)100=0.366≒1/3でもよい)
よって、正解は2。
1-1-1と同様に、
●AND条件(直列)は掛け合わせる・・・・A AND B → A*B
●OR条件(並列)は1から除したものを掛け合わせて最後に1から除する・・・・A OR B → 1-(1-A)*(1-B)
ということを覚えていて、応用できるかどうかの勝負です。
また、独立事象についてもよく理解しておく必要があります。そうでないと、
「1%×100=100%なので(1)」
とか、
「100回に1回壊れる。100単位時間だから100回なので、1回は壊れる。だから(1)」
といった間違いをしてしまいます。
たとえば、
「100枚のカードの中に1枚だけジョーカーが入っている。1枚カードを引くことを100回繰り返して、一度もジョーカーに当たらない確率は?」
という問題があるとします。
カードを引くたびに残りカードが減るのであれば、ロシアンルーレットになりますから、いつかはジョーカーを引きます。ですから一度も引かない確率はゼロです。でも、これは独立事象ではありません。なぜなら、カードを戻さないということは、2回目にはジョーカーを引く確率は1/100ではなく、1/99になっているからです。つまり、1回目の結果が2回目に影響を与えているからです。
独立事象であれば、カードを1回ひくたびに元に戻して100枚にして、シャッフルして、再度引くことになります。つまり、1回ごとにリセットします。
現実には独立事象というのは、そうそうあるものではありません。故障率1/100のシステムにしても、たとえばこれが機械なら、稼働時間が長引けば油が切れたりいろいろして故障率がアップしてきます。でも、独立事象と断ってありますから、たとえば1時間稼動するたびにオーバーホールして故障率を1%に調整して、また1時間稼動して・・・・という繰り返しをしているような状況になります。
戻る
2群 情報・論理に関するもの (全6問題から3問題を選択解答)
1-2-1 情報の圧縮に関する次の記述の中から、最も適切なものを選べ。
(1) 現在のデジタル情報は0と1の2値を1ビットとして表す方式が主流である。1ビットに多値の情報をもたせることにより、情報のビット数を減らし、情報を圧縮することができる。
(2) ワードプロセッサで作成した文書ファイルが大きすぎるときは、文字サイズを小さくすることにより、ページ数を減らし、ファイルの大きさを小さくして情報を圧縮することができる。
(3) ファイルに含まれる同じパターンの繰り返しなどの冗長さをとらえて短く表現することにより、情報を圧縮することができる。
(4) 情報を圧縮する専用ソフトウェアを用いればファイルの大きさは小さくなる。このソフトウェアを2回適用すれば、ファイルの大きさはさらに小さくなる。
(5) 紙に印刷すれば数千ページの文書も1枚のCD-Rに記録することができる。このように、重量や体積の小さな媒体に情報を格納することが情報圧縮の基本である。
正解は3
(1)・・・・×
1ビットは1ビット、0か1、OffかOnのデジタル情報の基本単位です。よって、1ビットに多値の情報を持たせることはできません。
(2)・・・・×
文字は1バイトまたは2バイトの情報で識別されるため、文字のフォントサイズと情報量は関係ありません。
たとえるならば、体の大きさの違う大男と小人でも、1人は1人。「人数」という物量は体の大きさとは関係ないようなものです。
(3)・・・・○
そのとおり。例えば、「1111111111」→「1が10回」というように表現文を短くしても意味は通じます。
これが一般的な圧縮技術の基礎理論で、ZipやLhaなどのアーカイブや、JPEGのような画像圧縮技術が、これを利用しています。
(4)・・・・×
上記(3)の理論を利用して圧縮しているため、ダブって圧縮しようとしても、2回目はほとんど小さくなりません。
(5)・・・・×
上記(3)より明らかなように、重量や体積は関係ありません。
よって3。
そもそも圧縮やアーカイブといった技術は、パソコンを道具としては使うけれど、動作原理とかソフトウェアのことなどに興味がなければ、知っている人は少ないでしょう。しかし、こういった情報技術の特定技術について正しく認識しているかどうかを問う問題は、頻繁に出ています。以前はエンコード・デコードなどの出題もありました。知っているかいないかの勝負ですから、知らなければ「しょうがない」と割り切ればいいでしょう。
戻る
1-2-2 レジスタを使い、符号付き二進数整数A(ただし、符号は正とする)の値を8で除算したときの商と余りを求めたい。次の空欄に当てはまる処理の組合せを選べ。
アルゴリズム
【商を求める】
・レジスタに値Aを入れる。
・3ビット(ア)し、値を取り出す。
【余りを求める】
・レジスタに値Aを入れる。
・7と(イ)演算を行い、値を取り出す。
|
(ア) |
(イ) |
| (1) |
左シフト |
論理和(OR)e |
| (2) |
左シフト |
論理積(AND) |
| (3) |
左シフト |
排他的論理和(XOR) |
| (4) |
右シフト |
論理和(OR) |
| (5) |
右シフト |
論理積(AND) |
正解は5
- 「レジスタ」について
まず「レジスタ」について理解しましょう。これは例えれば横にズラッと並んだ箱のようなものです。原稿用紙のマス目と思っても構いません。
たとえば「1000」という値をレジスタに入れてみましょう。ただしこれは2進数の値です。なぜならCPUが扱える情報は0か1の2進数だからです。
一番右の箱には1の位の数字(「1000」の一番右の文字)である「0」を入れます。
次に右から2番目の箱には10の位の値である「0」を入れます。
同じように右から3番めの箱には100の位の「0」を入れます。
最後に右から4番目の箱には1000の位の「1」が入ります。
イメージとしては下のようになります。以下の説明がしやすいように、「箱」は6つ用意しました。
左側2つの箱は空いていますが、これはここに0が入るのと同じです。すなわち、
としても同じです。
- 「シフト」について
「シフトする」とは、この箱に入っている数値を左右にずらすことです。
上の「1000」を、左に1つシフトすると、
となります。「1」が箱1個分左にずれましたね。実はその他の箱の「0」も全部左に箱1個分ずれています。この「箱1個分」を「1ビット」といいます。
さて、これで数値としては「10000」になりました。つまり、「左にnビットシフトする」とは、「n個分位を上げる」、あるいは「2n倍する」ということです。(10進数であれば10n倍ですが、2進数なので2n倍です)
次に、上の「1000」を、右に1つ(1ビット)シフトすると、
となります。「1」が1つ右にずれましたね。そして数値は「100」になりました。つまり、「右にnビットシフトする」とは、「n個分位を下げる」あるいは「2nで割る」ということです。
- 商を求める
以上を踏まえて、商を求めてみます。
たとえば10÷8=1余り2の計算を行ってみましょう。
まず、「二進数整数」とあるので、数値を2進数に変換します。
10進数の10は、2進数の1010です。これは、10=8+2=23+21、2進数で23=1000、21=10というように考えるとわかりやすいと思います。
この「1010」をレジスタ(箱)に入れてみましょう。
次にこれを、3ビット左または右にシフトしてみましょう。まず左にシフトしてみます。
なお、目印になるよう、4桁目の「1」を青く、2桁目の「1」を赤く色づけします。
今度は右にシフトしてみます。
結果、左シフト3ビットだと商が10000、右シフト3ビットだと1になるので、右シフトが正しいことがわかります。これで正解選択肢は(4)か(5)になりました。
- 余りを求める
10÷8=1余り2において、まず10(2進数1010)をレジスタに入れます。わかりやすくするため、4桁にします。
次に、これと7を、OR/XOR/AND演算します。
まず、10進数の7を2進数にしましょう。7は、4+2+1、すなわち22+21+1であり、2進数で22=100、21=10ですから、100+10+1=111です。
これをレジスタに入れると、
となります。
次に論理演算です。この場合、1010と0111について、「値がある」ということに関しての論理演算となります。
「OR」とは、「AまたはB」です。これが成立すれば1、成立しなければ0が、論理演算の答えとして返されます。
「1010」と「0111」の一番右の桁に注目しましょう。「1010」の一番右の桁は「0」ですね。すなわち値がありません。一方、「0111」の一番右の桁は「1」で、値があります(0ではありません)。OR演算なので、「1010の一番右の桁に値があるか、または、0111の一番右の桁に値がある」ということが成立すれかどうかになります。これは、「0111」の一番右の桁に「1」があるので、成立します。よって、一番右の位に関するOR演算の答えは1です。
同様に、2桁目を見てみます。「1010」は「1」、「0111」は「1」がそれぞれ入っています。どちらかに入っていれば条件成立ですから、成立します。よって、2桁目の演算結果も1です。
以下、3桁目も「0111」のほうに、4桁目は「1010」のほうに「1」が入っていますから、いずれも演算結果として1が返されます。
結果、OR演算結果は「1111」となります。
次にAND演算をしてみましょう。これは、「AかつB」であり、「1010」と「0111」どちらにも「1」が入っていなければ、演算結果として1は返されません。
1桁目は「0111」には「1」が入っていますが、「1010」のほうが「0」ですから、条件不成立で演算結果は0です。
2桁目は「1010」「0111」いずれにも「1」が入っていますから、条件成立で1が返されます。
3桁目、4桁目は、どちらかに「0」が入っているので、条件は不成立、0が返されます。
結果、AND演算結果は「0010」となります。
最後にXORです。これは、「Aでない・かつ・Bでない」です。つまり、「1010」と「0111」いずれにも「0」が入っていることが条件です。
このような桁はありません。ですから、XOR演算結果は「0000」になります。ちなみに、XOR演算結果は、OR演算結果と逆になります。
以上、OR演算結果は「1111」、AND演算結果は「0010」、XOR演算結果は「0000」でした。
これらは2進数ですから、これを10進数に直します。
「1111」は、23+22+21+1です。10進数で23=8、22=4ですから、8+4+2+1=15となります。
「0010」は、21ですから、10進数の2です。
「0000」は、0ですから、10進数でも0です。
以上より、「10÷8=1余り2」に合うのは、AND演算です。
以上のことから、シフトは右シフト、論理演算はANDでしたので、正解選択肢は(5)となります。
このように、「レジスタ」や「ビット」「シフト」といった用語の意味がわかり、論理演算を理解していれば、あまり悩むことなく解けますが、そういった用語となじみのない人は、入り口でギブアップでしょう。
戻る
1-2-3 デジタル時計などで使われる7セグメントのLED(発光ダイオード)がある。
LEDがO〜9の数字を等しい確率で表示するとき、ある数字(たとえば5)を見たときの情報量はlog210ビットである。
一方、LEDの上部のセグメントが故障している場合には、7は1と表示されるため、7と1を区別することはできない。この状態で1を見たときの情報量を選べ。
(1) log24ビット (2) log25ビット (3) log28ビット (4) log29ビット (5) log210ビット
正解は2
「5だとわかった」ということは、10個のうち、どれか1つであることが特定できたということですね。つまり、1/10の確率で起こる現象である「5が表示された」ことが確認できたわけです。
情報量の定義は、その事象が起こる確率をPとしたとき、-log2Pです。
ですから、5が表示された→1/10で起こる事象が認識された→-log21/10=log210ということで、情報量はlog210になります。
さて、1と7が区別できないということは、「1か7のどちらかが表示された」ということになります。1か7が表示される確率は2/10=1/5です。
ですから、情報量は-log2(1/5)=log25 です。よって正解は(2)。
1/Xの確率で起こす事象の情報量は-log21/X=log2X
ということを覚えておきましょう。
戻る
1-2-4 (ア)〜(ウ)は3種類のデータ探索手法の特徴を述べたものである。
(ア)探索時間を一定にできる。データの大小比較には適さない。
(イ)探索時間はデータ量に比例する。探索のための前処理は不要である。
(ウ)探索時間はデータ量の対数に比例する。更新処理の多い用途には適さない。
これらの特徴に最もよく当てはまる手法の組合せを選べ。
|
(ア) |
(イ) |
(ウ) |
| (1) |
ハッシュ探索 |
線形探索 |
二分探索 |
| (2) |
二分探索 |
線形探索 |
ハッシュ探索 |
| (3) |
二分探索 |
ハッシュ探索 |
線形探索 |
| (4) |
ハッシュ探索 |
二分探索 |
線形探索 |
| (5) |
線形探索 |
ハッシュ探索 |
二分探索 |
正解は1
探索法の基礎知識です。理解しやすいように、例題で考えましょう。
いま、子どもが40人いるとします。この中から身長140cmに一番近い子を探すとしましょう。
【ハッシュ探索】
各自の身長を、並び順(格納位置)に関連付けます。たとえば「身長から100を引いた残り」などです。この「身長から100を引いた残り」という式を「ハッシュ関数」といいます。
この場合、身長150cmなら150-100=50、152cmなら52、135cmなら35です。そして、それぞれが50番目、52番目、35番目に並べたイスに座ります。
当然ながら「空席」も出てきます。たとえば身長145cmの子がいなければ、45番目は空席となります。また2人座ることもあります。
実際にはこんな無駄なことはしませんが、「びっしり空間の無駄なく並べる」ことはできませんから、空間(コンピュータではメモリ)使用という点では若干ムダが出ます。ここで、効率はデータ数に支配されます。つまりデータが少ないと「空席」が増えますから、効率が悪くなります。
その代わり、ソートは早くなります。「140cmの子を探せ」と言われたら、140-100=40ですから、まっすぐ40番目のイスのところにいれば、その子が140cmに最も近いからです。つまり、探索時間は短く、しかも一定です。
そのかわり、データの大小比較には向いていません。「これ!」という条件のデータを見つけてくるのは得意です。
【線形探索】
子どもを適当に並べて、先頭から順番に探していきます。運がよければ1人目で見つかりますが、運が悪ければ40人目でやっと見つかります。したがって、探索時間はデータ量に比例します。また、3つの探索法の中では、平均的な探索時間は最大となります。
しかし、ハッシュ探索のようなハッシュ関数によるデータ格納位置の割り振りや、二分探索のようなソートは必要ありません。
【二分探索】
下準備として、背丈の順に40人並んだ列を作ります(ソート)。
最初に全体のちょうど真ん中、この場合は20人目でも21人目でもいいのですが、その子どもの身長を確認します。
140cmより低ければ、後ろの20人に着目し、140cmより高ければ前の20人に着目します。
そして着目したほうの20人のちょうど真ん中の子の身長を確認します。
140cmより低ければ、後ろの10人に着目し、140cmより高ければ前の10人に着目します。
そして着目したほうの10人のちょうど真ん中の子の身長を確認します。
140cmより低ければ、後ろの5人に着目し、140cmより高ければ前の5人に・・・・
というように探索を進めるもので、探索時間はデータ量の対数値に比例します。
線形探索よりは早く探索できますが、データの更新が頻繁にある場合は不向きです(せっかくソートしたのがやり直しになります)。
以上より、正解は(1)です。
戻る
1-2-5 インターネットに関する次の記述の中から、最も適切なものを選べ。
(1) www (World Wide Web)を公開するには必ず国への届出が必要である。
(2) wwwを構成するページ(Webページ)はすべての端末で同じレイアウトで表示される。
(3) 検索エンジンはインターネットに存在するすべてのWebページから検索を行う。
(4) URLに指定されたドメイン名は常にIPアドレスに変換されてから通信に使われる。
(5) wwwに書かれた内容は常に信頼できる。
正解は4
(1)・・・・× ドメイン取得ですが、そんな必要は一切ありません。
(2)・・・・× あり得ません。ブラウザにより異なります。
(3)・・・・× そんなことはありません。ロボット検索でも、どこからもリンクされていないページなどは検索されません。
(4)・・・・○ 「DNSによる名前解決」です。
(5)・・・・× そんなことはありません。常識でわかると思います。
「必ず」「すべての」「常に」というのは間違い選択肢のキーワードですが、この問題では全ての選択肢に使われていて、「択一セオリー」が通用しなくなっていますね。ネットに関する多少の知識があれば、消去法でたどり着けるでしょうが・・・・
戻る
1-2-6 情報ネットワークを通じて重要な情報を送信するときは、暗号化する必要がある。暗号に関する次の記述の中から、最も適切なものを選べ。
(1) 近年広く用いられている公関鍵暗号は、同一グループ内で送受信されている情報をそのグループに参加している者が共有することを主要な目的として用いられる。
(2) 近年広く用いられている暗号には、素数を鍵として用いるものがある。素数は有限個しか存在しないので、この方式は、将来は使えなくなる。
(3) 暗号化は2回行う(暗号文に再度同じ暗号化を施す)方が、1回行うより安全である。
(4) 暗号化の鍵はときどき変えることが、安全のために望ましい。
(5) デジタル署名は、暗号文が受信者に正しく届いたことを送信者に伝えるために、送信者のアドレスを数値化して暗号文の一部に埋め込んだものである。
正解は4
**********皆様からの情報・ご指摘*****megさんに情報をいただきました。ありがとうございます。
(1)公開鍵暗号は、利用者の身元についてCAなどの認証局が審査を行ったうえで公開鍵と秘密鍵を発行し、その異なる暗号を使って通信を行う人同士が暗号文の機密性、完全性、認証を実現することを主要な目的として用いられる。共有することを主目的にしているわけではない。
(2)素数は紀元前にユークリッドにより、無限個あることが示されている。有限個ではない。
(3)同じ暗号化の鍵を用いるため、2回行っても1回目より機密性が増すわけではない。
(4)DESでは52bitの鍵を用いるので、総当り法で暗号の解読が可能となる。RSAでは1024bitの素因数分解を利用しての鍵が用いられており、解読が難しくなっている。有効期限内でも、より安全を確保するためには時々鍵を変えることが望ましい。
(5)デジタル署名は、受信した内容が改ざんされていないこと(完全性)、本人から送られたものであること(認証)を証明すること。これにより、否認防止が可能となります。改ざんを検知するためのアルゴリズムとして、ハッシュ関数が用いられています。暗号文が正しく届いたことを送信者に伝えるためのものではない。
**********
戻る
3群 解析に関するもの (全フ問題から3問題を選択解答)
1-3-1 連続な関数f(x)について等間隔の格子点xi+1、x1、xi-1、xi-2の関数値をfi+1、fi、fi-1、fi-2と表すとき、格子点心における一階導関数の差分近似式として誤っているものを次の中から選べ。ただし、格子分割は等間隔で格子幅をδとする。
(1) (fi−fi-1)/δ
(2) (fi+1−fi)/δ
(3) (fi+1−fi-1)/2δ
(4) (fi+1−2fi+fi-1)/δ
(5) (3fi−4fi-1+fi-2)/2δ
正解は4
**********皆様からの情報・ご指摘*****aokiさんに情報をいただきました。ありがとうございます。
(導関数と差分近似式について)
導関数とは微分係数の変化を表す係数で、一般式では
f’(x)=lim(h→0)〔f(x+h)−f(x)〕/h となります。lim(h→0)によりこの式の分子・分母ともに限りなく0に近づき、瞬間変化率が算出されます。厳密解であり、グラフでは接線の勾配を表します。
差分近似式は解析領域を規則正しい格子によって分解し、微分を例えば格子の幅δに対して
f’(x)の差分近似式=〔f(x+δ)−f(x)〕/δ となります。
導関数の式からlim(h→0)を外した形となり、格子幅δ当たりの平均変化率、グラフでは、x1からxi+1までの平均勾配と考えればよい。。
本題では、題意「xi+1、x1の関数値をfi+1、fiとする」からfi+1=f(xi+1)、fi=f(x1)。
題意「格子幅δ」からxi+1=x1 +δ。これらを(2)の式に代入すると、
(2)の式 (fi+1−fi)/δ
=〔f(xi+1) −f(x1)〕/δ
=〔f(x1 +δ)−f(x1)〕/δ
がこの形となります。
格子幅δを小さくすることにより厳密解に近づき、近似誤差が小さくなります。
(1)は、xi-1からx1までの格子幅δ当たりの平均変化率。グラフでは平均勾配。
(2)は、x1からxi+1までの格子幅δ当たりの平均変化率。グラフでは平均勾配。
(3)は、xi-1からxi+1までの格子幅2δ当たりの平均変化率。グラフでは平均勾配。
〔(fi−fi-1)/δ+(fi+1−fi)/δ〕/2 の形となり、(1)と(2)の平均でもあります。
(4)は、(fi+1−fi)/δ−(fi−fi-1)/δで(1)−(2)の形。
この式は、即ち、近似値−近似値の形(勾配で表せば平均勾配−平均勾配の形)となり、近似式ではない、と推測でき、誤り。」
これで正解は(4)。
(5)は時間がかかり、考えなくてよろしい。
(次式は臨時掲示板、合格希望様のレスです。)
(5)=(fi - fi-2)/2δ + (fi - fi-1)/δ - (fi-1 - fi-2)/δ
(fi - fi-2)/2δは、xi-2からx1までの格子幅2δ当たりの平均変化率。グラフでは平均勾配。
(fi - fi-1)/δは(1)の形。
(fi-1 - fi-2)/δは、xi-2からxi-1までの格子幅δ当たりの平均変化率。グラフでは平均勾配。
平均勾配+平均勾配−平均勾配の形となり、差分近似式となる。
(別解)簡単な事例で計算してみる方法。
f(x)=x、δ=1、x1=10(xi+1=11、x1=12、xi-1=9、xi-2=8)として、計算してみる。
(1)式=(10-9)/1=1 、(2)式=(11-10)/1=1 、(3)式=(11-9)/2=1 、(4)式=(11-20+9)/1=0 、(5)式=(30-36+8)/2=1
(4)だけが0になり、正解は(4)。
「簡単な事例(1とか、両端の数字など具体的な数字、式)にて計算してみる」解法に慣れましょう。
**********
**********皆様からの情報・ご指摘*****megさんに情報をいただきました。ありがとうございます。
格子幅(△x)がδの時、連立一次関数f(xi)=fi , f(xi+δ)=fxi+1で表される。
f(x)=xとし、xi=1 , δ=1 と仮定すると f(xi)=fi=1 , fi+1=2 , fi-1=0 ,fi-2=-1となる。
格子点における一階導関数の差分近似式は、 df(xi)/d(x)=0 とはならないため、
上記数値を代入して、0となる(4)が誤っている。(4)以外はすべて1。
**********
戻る
1-3-2 数値解析の誤差に関する次の記述のうち、最も適切なものを選べ。
(1) 浮動小数点演算において近接する2数の引き算では、有効桁数が失われる桁落ち誤差を生じることがある。
(2) 非線形現象を線形方程式系で近似しても、線形方程式の数値計算法が数学的に厳密であれば、得られる結果には数値誤差はないとみなせる。
(3) テイラー級数展開に基づき微分方程式を差分方程式に置き換えるときの近似誤差は、格子福によらずにほぼ一定値となる。
(4) 有限要宗法の要素分割を細かくすると近似誤差は犬きくなる。
(5) 数値計算の誤差は対象となる物理現象の法則で定まるので、計算アルゴリズムを改良しても誤差は減少しない。
正解は1
**********皆様からの情報・ご指摘*****aokiさんに情報をいただきました。ありがとうございます。
(1)・・○ 浮動小数点演算過程で、絶対値のほぼ等しい数の差を計算したときに有効桁数が大幅に減少するための誤差を「桁落ち誤差」と言います。
(2)・・× 数値解析法は厳密な数学では解決できない分野における近似誤差を伴う計算法です。数値解析法はあくまで「近似解」であり、「厳密解」でないことを理解しましょう。
(3)・・× 格子幅が小さいほど計算回数が増え、近似誤差が小さくなることは数値解析法の趣旨を理解していれば推測できます。
(4)・・× 要素分割を細かくすると計算回数が増え、近似誤差が小さくなります。
(5)・・× (3)(4)のように格子幅、要素分割を細かくするだけでも近似誤差が減少します。
(固定小数点演算と浮動小数点演算について)
固定小数点演算は、有効桁数にかかわらず小数点の位置を決めて演算します。経理計算(すべて円止め)や工事数量計算(すべて小数第2位止め)の場合に便利です。
これに比して浮動小数点演算は、7812000を7.812*106、0.07812を7.812*10-2とa*10n(10進数の場合)の形により表現します。
これにより表現可能な数値の範囲を広くでき、技術計算で多く用いられています。電卓にも浮動小数点と固定小数点演算用とあります。
(「桁落ち誤差」はどのような場合に生じるのか:)
鉄道などの走行時間において、ダイヤルとの差(遅延時間)を求める場合、最初の駅から最後の駅までの「全実走行時間−全ダイヤル時間」で算定すると、「ほぼ等しい数の差を計算」することになり「桁落ち誤差」が生じることがあります。各駅間における「実走行時間−ダイヤル時間」を算定してそれを集計すれば誤差が少なくなります。
国道○号の1234.123キロ程(起点からの距離をkmで表す)から1235.345キロ程までの距離を有効桁数4桁の浮動小数点演算をしますと、有効桁数4桁のため1235−1234=1kmとなり、有効桁数1桁に減少します。これを「1230キロ程から5.345km地点と1230キロ程から4.123km地点との距離」として計算しますと5.345−4.123=1.222kmとなり、有効桁数4桁になります。
「不動小数点の誤差」には、「情報落ち誤差」(絶対数の非常に大きな数と小さな数の加減算を行った場合、小さい数が計算結果に反映されない誤差)もあります。情報落ちを防ぐためには、複数の多くの加減算では絶対値の小さい順に値を並べ替えて順次計算すること。
**********
戻る
1-3-3 下図のような一次元トラスの有限要素モデルを考える。
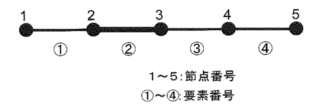
図1 一次元トラスモデル
この場合、全体剛性マトリクスは5行5列の正方マトリクスである。ここで、上図のように要素(2) のみ補強する。5行5列の全体剛性マトリクスの成分で変化するのは次のどれか。なお、(i、j)は剛性マトリクスのi行j列の成分を表す。
(1) (2,2)
(2) (3,3)
(3) (2,2), (3, 3)
(4) (2,2),(3,3),(2,3)
(5) (2,2),(3,3),(2,3),(3,2)
正解は5
以下、臨時掲示板より邪bさんのレスです。
補強前のバネ定数をk, 補強後のバネ定数をKとすると、
補強前は、
s22=2k,s23=-k,
s32=-k,s33=2k
補強後は、
s22=k+K,s23=-K
s32=-K,s33=k+K
戻る
1-3-4 Nはξ、η、ζの関数とする。すなわち, N=N(ξ、η、ζ)と表すことができる。また、ξ、η、ζとx、y、zの間にはx=x(ξ、η、ζ)、y=y(ξ、η、ζ)、z=z(ξ、η、ζ)の関係があるとする。このとき、Nのξ、η、ζに関する偏微分と、Nのx、y、zに関する偏微分との間には次のような関係式が成り立つ。

下記の中から間違っているものを選べ。
(1) (1)は∂x/∂ηである。
(2) (2)は∂y/∂ηである。
(3) (3)は∂z/∂ζである。
(4) (4)は∂z/∂ξである。
(5) (5)は∂x/∂ζである。
正解は1
(1)は∂x/∂ξですね。これは私でもわかりました。^^;
戻る
1-3-5 下図に示すように、左端を固定された長さL、断面積Aの棒が右端に荷重Pを受けている。この棒のヤング率をEとしたとき、棒全体に蓄えられるひずみエネルギーはどのように表示されるか。次の中から選べ。

(1) P/2AE (2) P/A (3) P2L/2AE (4) PL/2AE (5) P2/2A2E
正解は3
臨時掲示板より、blueさんのレスを引用します。
解法1
荷重PがかかったときのひずみがP/AEなので、変位はPl/AE
横軸変位、縦軸荷重のグラフを書くと、蓄えられたエネルギーは
直角三角形であらわされるので、Pl/AE×P=P^2l/2AE → (3)
解法2
各選択肢の単位を見ると、
(1)無次元 (2)Pa (3)J (4)m (5)Pa
よって(3)
戻る
1-3-6 一定の高い圧力を持った気体を密閉する円筒容器の応力解析を線形弾性微小変形理論に基づいた有限要素法で行うに際して、材料の縦弾性係数(ヤング率)に実際の値よりも大きな値を代入してしまった。このときに得られた最大応力と最大径変化量の記述に関して、次の中から正しいものを選べ。
(1) 応力は正しいが、径変化量は実際上りも大きい。
(2) 応力は正しいが、径変化量は実際よりも小さい。
(3) 径変化量は正しいが、応力は実際よりも大きい。
(4) 径変化量は正しいが、応力は実際よりも小さい。
(5) 応力、径変化量とも正しくない。
正解は2
ヤング係数が大きいと変形量は小さくなるので、(2)と(5)以外は全部間違いです。
しかし最大応力は変形しやすさとは関係ないので、ヤング率が変わっても最大応力は変わりません。
戻る
1-3-7 下図に示すように2種類の固体材料A、Bからなる壁の両面が加熱、冷却されている。
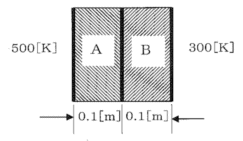
このとき、壁内部の温度分布を表すグラフとして最も適切なものを選べ。ただし、材料A、Bの内部材質は均一で熱伝導率はそれぞれ1.5[W/mK]、0.5[W/mK]で、厚みはいずれも0.1[m]とし、加熱・冷却面の温度はそれぞれ500[K]、300[K]とする。
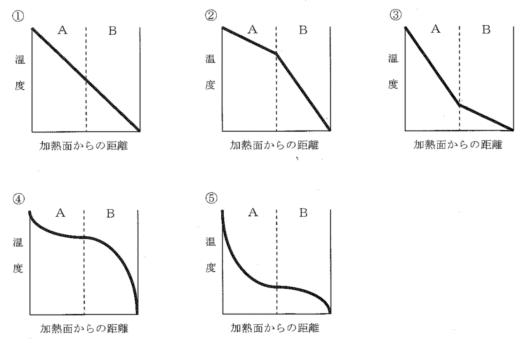
正解は2
材質が均一なので、熱伝導率も一定、よって温度勾配も一定ですから、グラフは直線で構成されます。よって、(1)=(3)のいずれか。
熱伝導率が大きいということは、熱が伝わりやすいということなので、熱伝導率が大きいほうが表裏の温度は近くなります。すなわち、グラフの勾配は小さくなります。よって、熱伝導率が大きいAの部分の勾配がゆるい(2)が正解です。
臨時掲示板での議論は大変参考になります。こちら
戻る
4群 材料・化学・バイオに関するもの (全6問題から3問題を選択解答)
1-4-1 化学結合は、いくつかに分類できる。以下のように、「結合の名称−結合の形成に深く関わる事項一具体的な物質」を順に組み合わせるとき、誤りを合むものを選べ。
(1) イオン結合 − 静電引力 − 塩化ナトリウム
(2) 共有結合 − 共有電子対 − 二酸化ケイ素
(3) 金属結合 − 自由電子 − カルシウム
(4) 水素結合 − 極性 − フッ化水素
(5) 配役結合 − 非共有電子対 − グラファイト
正解は5
グラファイトは、要は石墨です。六角形の「板」がいっぱい重なったような、金属光沢のある黒色不透明の六角板状結晶です。
結合としては、共有結合(面内共有結合)です。
戻る
1-4-2 次の元素やイオンの中から、M電子殼内の電子数が最小の値(0を含む)をとるものを選べ。ただし、元素記号の左下の数値は、原子番号である。
(1) 11Na (2) 13Al3+ (3) 15P (4) 17Cl (5) 19K+
正解は2
電子殻内に入る電子数は、Kが2個、Lが8個、Mが18個、Nが32個)、Oが50個、Pが72個です。
電子数は単純に原子番号と同じなので、たとえば(1)は電子が11個ですから、KとLは満杯で、Mに1個入ります。
(2)は13個なのですが、3+なので、電子は3個少なく、13−3=10。KとLでちょうど10個入りますから、Mには0個です。
同様に、(3)は15個でMに5個、(4)は17個でMに7個、(5)は19−1=18でMに8個です。
よって、正解は(2)。
電子殻と電子数は単なる知識ですが、原子・分子に関する基礎的知識の1つではあります。
戻る
1-4-3 無機材料の機能に関する次の記述のうち、最も適切なものを選べ。
(1) 無機材料の熱膨張率は結合様式によって異なる。原子の充填構造が密であるほど、熱の吸収による原子の格子振動を緩和しやすくなり、熱膨張率は小さくなる。
(2) 水酸アパタイトは骨や歯などの生体骨組織と類似しており、生体親和性に優れたインプラント材料である。水酸アパタイトは、酸性水溶液中で難溶性であることを利用して粉体が合成される。
(3) 発光ダイオードでは、化合物半導体のpn接合の順方向に電圧をかけて、pn接合領域から電子をn型領域へ、正孔をp型領域へと移動させると発光する。
(4) ニッケル−水素化物二次電池の負極には、水素吸蔵合金が用いられている。充電時には、合金中へ水素が取り込まれ、逆に放電時には合金から放出される。
(5) ダイヤモンドは、電気伝導性、熱伝導性は低く、硬度は高いという特徴を特っており、超硬材料として切削工具等に広く使われている。
正解は4
(1)・・・・×
(2)・・・・× アパタイトは石灰と同じく、酸性で溶け、アルカリに難溶です。
(3)・・・・×
(4)・・・・○ その通り。
(5)・・・・× ダイヤモンドは極めて熱伝導が高く、ニセモノを見分ける簡易判定法として、ハーッと息を吹きかけて曇りがすぐ取れたらホンモノ、というのがあります。また、絶縁体でもあります。
(1)、(3)について解説できる方がいらっしゃいましたら、ぜひお願いいたします。
**********皆様からの情報・ご指摘*****megさんに情報をいただきました。ありがとうございます。
(1)は原子のずれが小さいため、緩和ではなく抑制しやすくなる。逆に、充填構造が密でない原子の場合は、結合力が小さいため振動による原子のずれが生じやすく、熱膨張率が大きくなる。
(3)はn型とp型の記述が逆。pn接合にエネルギーを与えると、電子はp型へ、正孔はn型へ移動し、電子と正孔の対が発生する。これを電荷の分離とよび、pn接合の両端に電位差が生じるため、起電力により発光する。
(4)は負極では、LaNi5H6⇔LaNi5+6H2O の化学反応が起こるため、充電の時は水素が取り込まれ、放電の時は水素が放出される。
**********
戻る
1-4-4 資源と金属製造に関する次の記述の括弧内に入る金属の組合せとして最も適切なものを選べ。
金属の地殻中の存在量は、(1)が(2)より多いが、年間世界生産量は(2)の方が多い。(3)は埋蔵量が少なく可採年数も短いため、資源節約の面からみればリサイクルの重要性が商い。金属製造のための鉱石は、ほとんどが酸化鉱であるが、(3)は硫化鉱、(4)は炭酸塩鉱も原料となる。反応性に富む卑金属は、炭素や水素を用いた普通の還元法では金属採取が困難であるため、(1)、(4)は溶融塩電解法が工業化されている。また、(5)は、電解法で作製した(4)を使って、塩化物から金属への還元が行われており、トンあたりの価格も(5)が最も商い。
|
(1) |
(2) |
(3) |
(4) |
(5) |
| (1) |
Al |
Fe |
Zn |
Mg |
Ti |
| (2) |
Al |
Mg |
Zn |
Fe |
Ti |
| (3) |
Ti |
Fe |
Al |
Mg |
Zn |
| (4) |
Ti |
Fe |
Al |
Zn |
Mg |
| (5) |
Ti |
Mg |
Al |
Fe |
Zn |
正解は1
チタンはかなり希少なほうなので、これが鉄やマグネシウムより多いということはありません。対して、アルミニウムは鉱物の基本構成であるところのアルミナ(Al2O3)を作るので、かなり量は多くなります。よって、正解は(1)か(2)に絞れます。
(1)と(2)の違いは、鉄とマグネシウムのところですが、単純に鉄とマグネシウムの生産量を考えれば、鉄のほうがおおいと想像できます。というか、マグネシウムがアルミニウムより生産量が多いとは思えません。
というような考察で(1)に絞り込めます。
戻る
1-4-5 DNAの変性について述べている次の文章の括弧内に入る語句の組合せとして最も適切なものを選べ。
二本鎖DNAを熱や強アルカリで処理すると、変性して一本鎖となる。DNAを徐々に加熱していくと変性の度合いに応じて(1)の吸収量が増加する。DNA分子の(2)が変性する温度を融解温度といい、グアニンと(3)の含量が多いほど高くなる。熱変性したDNAをゆっくり冷却すると再び二重らせん構造に戻るが、これを(4)という。
|
(1) |
(2) |
(3) |
(4) |
| (1) |
紫外線 |
半分 |
ウラシル |
メルティング |
| (2) |
紫外線 |
半分 |
シトシン |
アニーリング |
| (3) |
紫外線 |
全部 |
シトシン |
メルティング |
| (4) |
可視光線 |
半分 |
ウラシル |
アニーリング |
| (5) |
可視光線 |
全部 |
シトシン |
メルティング |
正解は2
以下、私の解答例です。
とりあえずDNAなので、ウラシルはそもそも入っていない。だから(1)と(4)は除外。
冷却により二重らせんに戻る現象を「アニーリング」というか「メルティング」というかだが、「メルティング」は「メルト」つまり溶けるということだから、「融解」ならともかく、二重らせん復活の現象に使うことはないだろう。だから(2)が残る。
知識がちゃんとあれば言うことなしですが、そうでなくても、上記のように解くことはできます。
戻る
1-4-6 タンパク質の性質について述べている次の記述のうち、最も適切なものを選べ。
(1) タンパク質を構成するアミノ酸はほとんどがD体である。
(2) タンパク質は、アミノ酸同士がエステル結合によってつながったものである。
(3) α−ヘリックス(らせん)は特定のタンパク質に見られる二次構造である。
(4) 疎水性相互作用は、タンパク質の立体構造の維持にとても重要である。
(5) 電荷を持たないアミノ酸の側鎖はクンパク質の表面に分布していることが多い。
正解は4
臨時掲示板のレスを参考にします。
(1)・・・・× 生体内のアミノ酸はL体。
(2)・・・・× アミノ酸同士の結合はペプチド結合。
(3)・・・・× αヘリックスは多くのタンパク質に見られる普遍的な2次構造。
(4)・・・・○ その通り。
(5)・・・・× タンパク質はたいてい水溶性で、表面には電荷を持ち親水性なアミノ酸が多く露出していることが多い。一方、内部は疎水環境にあり電荷を持たない疎水性アミノ酸残基同士が寄り集まっている。
戻る
5群 技術連関 (全6問題から3問題を選択解答)
1-5-1 エネルギー消費を伴う次のような行動に伴って排出される1人当たりの二酸化炭素(C02)の量について、大小関係の正しいものはどれか。ただし、ガソリンの比重は0.75とし、ガソリン1kgに含まれる炭素(C)は0.85kgとする。また、電力1kWhの消費に伴って発電所で排出される二酸化炭素(CO2)は0.36kgとする。
a:燃費10km/リットルのガソリン自動車に2人が乗車して100km走行したときの1人当たりの排出量
b:平均消費電力8,000kW、平均時速200kmの高速鉄道車両1編成に1,000人が乗車して、500km走行したときの1人当たりの排出量
c:4人家族の世帯が、消費電力500Wの暖房器具1台を、1日当たり4時間の割合で50日間使用したときの1人当たりの排出量
(1) a>b>c
(2) a>c>b
(3) b>a>c
(4) c>a>b
(5) c>b>a
正解は2
(aの排出量について)
燃費10km/リットル&100km走行で、消費量は10リットル。比重0.75なので、7.5kg。ガソリン1kg中に0.85kgなので、0.85×7.5=6.375kg。
炭素の原子量は12、酸素は16なので、CO2にすると、6.375+(6.375×16/12)×2=23.375kg。2人なので1人あたりは11.6875kg。
※この部分は、炭素の原子量12、二酸化炭素の分子量44にて6.375×44/12=23.375kgとしてもかまいません。
(bの排出量について)
500km÷200km/h=2.5h。消費電力8,000kWにて、8,000×2.5=20,000kWh。1kWhに伴いCO2が0.36kg排出されるので、20,000kWhなら、7,200kg。
1,000人なので、1人あたりは7.2kg。
(cの排出量について)
500W×4h/日×50日=100,000Wh=100kWh。1kWhに伴いCO2が0.36kg排出されるので、100kWhなら36kg。4人なので、1人あたりは9kg。
以上により、bが最小、aが最大。すなわち、a>c>bとなって、正解は(2)。
aの排出量計算が、数字が細かくてやや面倒なのと、原子量を知らないと計算できないという、ワナがかけてあります。bとcは暗算でもできる程度の計算なので、この大小関係(c>b)を出せば、(1)と(3)は除外できますが・・・・
酸素や炭素などのごく一般的な元素については、原子量は覚えていたほうがいいと思います。
戻る
1-5-2 廃棄物処理・リサイクルに関する国際条約および我が国の法律に関する以下の記述についての正誤の組合せとして最も適切なものを選べ。
a)循環型社会形成推進基本法は、焼却するごみの量を減らすことを目的に、リサイクルを最優先とする社会の構築を目指した法律である。
b)容器包装リサイクル法(容器包装に係る分別収集及び再商品化の促進等に関する法律)では、PETボトル、スチール缶、アルミ缶、ガラスびんの4品目について、リサイクル(分別収集及び再商品化)のためのすべての費用を、商品を販売した事業者が負担することを義務づけている。
c)家電リサイクル法(特定家庭用機器再商品化法)では、電子レンジや冷蔵庫などの主な家電製品について、リサイクルのための費用を製品の購入時にあらかじめ消費者が負担することが義務付けられている。
d)バーゼル条約(有害廃棄物の国境を越える移動及びその処分の規制に関するバーゼル条約)は、発展途上国から先進国へ有害廃棄物が輸入され、環境汚染を引き起こした事件を契機に採択されたものであるが、リサイクルが目的であれば、目本から発展途上国に有害廃棄物を輸出することは規制されてはいない。
|
a |
b |
c |
d |
| (1) |
正 |
正 |
正 |
正 |
| (2) |
正 |
正 |
正 |
誤 |
| (3) |
誤 |
正 |
誤 |
正 |
| (4) |
誤 |
誤 |
正 |
誤 |
| (5) |
誤 |
誤 |
誤 |
誤 |
正解は5
a・・・・× リサイクル優先ではなくリデュース(ごみを出さない)、リユース(もう一度使う)ことが優先です。
b・・・・× 容器包装リサイクル法対象容器は、商品消費・分離後は不要となる「容器」および「包装」であり、紙やダンボールなども含まれます。
c・・・・× 冷蔵庫・洗濯機・エアコン・テレビの4品目が対象であり、電子レンジは対象外です。また、購入時ではなく廃棄時です。
d・・・・× バーゼル条約で禁じられているのは、先進国から途上国への有害廃棄物移動です。
戻る
1-5-3 温室効果と気候変動に関する次の記述について、正しいものを選べ。
(1) フロン類のうちCFCとHFCはオゾン層破壊物質としてモントリオール議定書で生産が規制されている。一方、HCFCはオゾン層を破壊しないが強力な温室効果ガスであるため、モントリオール議定書ではなく京都議定書で削減数値目標が定められている。
(2) IPCC(気候変動に関する政府間会合)第三次評価報告書によれば、人為的な温室効果ガス濃度の上昇による気候変動は、過去2万年間に生じた自然的な変化と比べても急速なものであり、低緯度付近に比べて極地に近づくほど気温上昇が激しくなる。
(3) 気候変動枠組条約では、最終目標として「大気中の温室効果ガスの濃度を地球の気候に悪影響を与えないような濃度レベル」に抑えることを決めている。これを受けて、京都議定書では、2008年〜2012年の5年間に付属書I国全体で、温室効果ガスを、基準年で排出していた量より、少なくとも10%削減することを定めた。
(4) 地球の表面温度は太陽から降り注ぐエネルギーと、宇宙空間へ放射するエネルギーのバランスによって決まる。大気中にある温室効果ガスには、地球が宇宙空間へ放射するエネルギーを吸収し、一部を地表面に戻すことで地面を暖める作用がある。もし、大気中に温室効果ガスが全く存在しなければ、地球表面の平均気温は産業革命以前の平均気温に戻ると推定される。
(5) 京都議定書は2005年2月に発効したが、世界のCO2排出量の中で国家として一位と二位を占める米国と中国は、京都議定書から離脱している。
正解は2
(1)・・・・× 1992年11月の第4回締約国会議で、フロン代替物質のハイドロクロロフロロカーボン(HCFC)の生産を2019年末までに実質廃止し、2029年までに全廃することを決めています。
(2)・・・・○ その通り。
(3)・・・・× 京都議定書では、先進国全体の温室効果ガスの排出量を、2008年〜2012年の間に、1990年の水準より5%削減を目的として、先進各国の削減目標を設定しています。
(4)・・・・× 温室効果ガスは二酸化炭素やメタンなど、自然界にもともと存在するガスが主体ですので、これが「全くなくなった」場合、産業革命以前どころか、はるかに低くなります。
(5)・・・・× CO2排出量は米国1位、中国2位ですが、中国は京都議定書を批准しています(こちら)。いかに米国が「ならず者」であるかがよくわかります。
戻る
1-5-4 アイデア創出法の一つにブレインストーミングと呼ばれる方法がある。ブレインストーミングでは、参加者が4つのルールを守りながら、会議形式でアイデアを出す。次に掲げた4つのルール中の( )に入る言葉の組合せとして、最も適切なものを選べ。
ルールA:他の参加者から出たアイデアに対する批判(ア)
ルールB:自由奔放な発想(イ)
ルールC:(ウ)を求む
ルールD:他の参加者から出たアイデアの組合せ・改善(エ)
|
(ア) |
(イ) |
(ウ) |
(エ) |
| (1) |
を歓迎 |
お断り |
質より量 |
を歓迎 |
| (2) |
を歓迎 |
を歓迎 |
量より質 |
お断り |
| (3) |
お断り |
を歓迎 |
質より量 |
を歓迎 |
| (4) |
お断り |
お断り |
量より質 |
お断り |
| (5) |
お断り |
を歓迎 |
量より質 |
を歓迎 |
正解は3
ブレインストーミングは、合意形成などでも基本的な手法ですので、その特徴は覚えておいたほうがいいでしょう。単純に言うなら、「何でもいいから思いついたこと・連想したことをじゃんじゃん発言する」ということです。
したがって、他人の批判は厳禁です。Bは当然歓迎。人の発想からの発展形も大歓迎です。あとは(ウ)ですが、とにかく発言量を期待します。質を求めると発言が減ります。(特定のレベルの高い人に偏ってしまいます)
よって正解は(3)。
戻る
1-5-5 ある工場では生産能力増強のため新規に生産設備を導入することにした。候補としては2種類の生産設備A、Bがあり、両設備は同じ機能を有し、同じ耐用年数で、使用後の処分価格は共にゼロ円とする。また、設備Aの価格は500万円、設備Bの価格が600万円であり、製品1個当たりの変動加工費は設備Aでは600円/個、設備Bでは500円/個である。このとき、どちらの設備を導入すべきかを経済性の面から検討した。検討結果の意見として最も適切なものを選べ。ただし、金利、税については考慮対象外とする。
(1) 製品の生産量にかかわらず、価格の安い設備Aを導入すべきである。
(2) 耐用年数内の製品生産量が1万個未満では設備Aを、1万個を超える湯合は設備Bを導入すべきである。
(3) 耐用年数内の製品生産量が5万個未満では設備Aを、5万個を超える場合は設備Bを導入すべきである。
(4) 耐用年数内の製品生産量が6万個未満では設備Aを、6万個を超える場合は設備Bを導入すべきである。
(5) 製品の生産量にかかわらず、変動加工費の安い設備Bを導入すべきである。
正解は2
要は、Aは初期コストが安いがランニングコストが高く、Bはその逆ということになります。
こういう問題では、費用を計算したりする前に、まず選択肢を見ましょう。場合によっては計算しなくても答えが絞れるかもしれません。
(1)は、初期コストだけで決めなさいということで、そんなことはあり得ません。ですから×。
(2)〜(4)は同じようなことを言っています。これは計算しないとわかりません。
(5)は、ランニングコストだけで決めると言っていますから、そんなことはあり得ません。ですから×。
さて、コスト計算ですが、製品生産量をX個とすると、
設備Aの費用CA=500万円+600X
設備Bの費用CB=600万円+500X
となります。CAとCBがイコールとなるXが「分かれ目」ですから、CB-CA=0とすれば、100万円−100X=0、よってX=10,000となり、(2)が正解です。
このようにXを算出することが思いつかなければ、当てはめ計算をして比較します。1万、5万、6万と、(2)と(3)の間の差が大きいので、(2)と(3)を比較します。
(2)A:1100万円 B:1100万円
(3)A:3500万円 B:3100万円
となるので、(2)が正解です。
戻る
1-5-6 科学技術の進展と日常生活への浸透とともに、専門的な領域と一般社会との関係をさらに密接にしていくことが望まれている。このことに関して、近年「科学技術コミュニケーション」と呼ばれる領域の重要性が指摘されている。科学技術コミュニケーションの領域や活動内容などを表したものとして、次の記述のうち最も適切なものを選べ。
(1) 基礎的な科学と応用的な技術領域とが、より頻繁かつ実質的に情報を共有することを科学技術コミュニケーションと称し、このような用語こそなかったものの、古代ギリシア時代から盛んに行われていたことである。
(2) マスメディアには、しばしば科学や技術に対する理解不十分な記述が散見される。このような記述をなくすために、マスメディアの製作にもっと科学技術を駆使するべきである。科学技術によるメディア・コミュニケーションが必要である。
(3) 科学者や技術者たちは、学会発表や専門論文の執筆を通して、同じ領域の専門家に情報を伝達するが、そのような専門的なコミュニケーションの方法は一般社会とのコミュニケーションにそのまま使えるものである。
(4) 科学者や技術着たちが専門的な情報を発信するだけでは、社会にはなかなか受け人れられない。社会的ニーズや非専門家にとっての有効性などを理解し、科学技術と社会との双方向コミュニケーションを促進することが必要である。
(5) 人間のコミュニケーションは言語によるものだけではない。非言語コミュニケーションも含め、人間のコミュニケーションを円滑に促進するための科学技術を開発する領域が、科学技術コミュニケーションと呼ばれるものである。
正解は4
(1)・・・・× 科学技術コミュニケーションとは、社会の科学技術リテラシーを高めるため、専門家や一般市民、行政その他、様々な立場の人がコミュニケーションを持とうとする活動のことです。問題文を読めば、この選択肢は誤りなのは一目瞭然です。
(2)・・・・× マスメディア政策への科学技術の駆使と、科学技術への理解の増進は、強く関係するものではありません。
(3)・・・・× 一般の人向けには、当然ながら表現方法など様々な情報伝達上の工夫が必要になります。
(4)・・・・○ その通り。
(5)・・・・× これも科学技術コミュニケーションの定義になりますが、用語の並び(「科学技術」と「コミュニケーション」)から、こういうコミュニケーション技術に関する言葉ではなく、コミュニケーションの種類・あり方であることがわかると思います。
戻る





