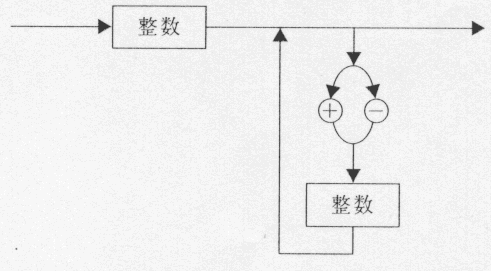
�@�E����0�ɁA����1000�ɏ���������B
�@�E���������������������B
�@�E�ȉ��̊��ʓ��̎菇������J��Ԃ��B
�@�@�@{�Ex��0����1�̊Ԃ̗�����������B
�@�@�@ �E����0����1�̊Ԃ̗�����������B
�@�@�@ �E�����m�A�n�Ȃ�A���̒l��1������������B�p
�@�E��/����4�{����B
(1)�@���{�����P
(2)�@�����P�������P
(3)�@�������{���������P
(4)�@�������{���{�����P
(5)�@�������{���������P
�āF�R
�v�́A���̂悤�Ȃ��Ƃ�����Ă���B
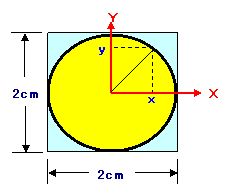
�E�}�̂悤�ɁA�~�̒��S�����_�ɂ���XY���W���l����B
���C����0�`1�܂ł̃����_���l������Ƃ������Ƃ́A����1�A����1�Ő����`�̒[������A�����`�̒��ɂ͕K���u�j��������v�B
����ɉ~�̒��ɂ�����J�E���^�i�ϐ����j��1�A�b�v�B
�~���ɓ������ꍇ�A���a1cm�ȓ��A���Ȃ킿���_����̋�����1cm�ȓ��Ƃ������ƁB
���_����̋���L�́AL=��x2+y2�����AL��1cm�Ȃ̂ŁA�������āA��2+��2��1�ł��悢�B
�Ȃ��A�ȒP��BASIC�v���O�����ɂ���Ɖ��L�̂悤�ɂȂ�i�v���O�����ɂł��Ă��������킩��킯�ł͂Ȃ����j�B
n=0:m=1000
for I=1 to m
x=RND:y=RND
if x*x+y*y<1 then n=n+1
next I
print 4*n/m
**********�F�l����̏��E���w�E*****aoki����ɏ������������܂����B���肪�Ƃ��������܂��B
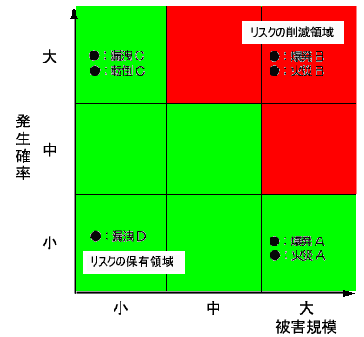
���Z���w�́A�܂��́A�O���t���������Ƃł��B����ɂ����̊T�v�����߂܂��B
�u���a�P�̉~�v�w�Q �{�x�Q���P�̃O���t�y�ѐ����`�̐}��`���B
�u�~�ɓ���v�E�E�E�E�~�̒��̗̈�́@�w�Q �{�x�Q�@���P�ł���܂��B
�́i�R�j�炵���B
���Ƃ́A�ߓǂ݂Łu�m���^�S�v�̈Ӗ����m�F�B�u�V���~���[�g�v�u�����v�̌��t��[���l���Ȃ��Ă��悢�B
**********
����������Ă���̂��A�e�ϐ�������\���Ă��邩���p�b�Ƃ킩�邩�ǂ��������ł��B�E�}�̂悤�ȃC���[�W�������ׂ�OK�B
�E���̃J�[�h���n�[�g�ł��邱�Ƃ�m�������̏��ʂ�
�@�@�@�@�@log24��2bit
�@�ł���B
�E���̃J�[�h���L���O�ł��邱�Ƃ�m�������̏��ʂ�
�@�@�@�@�@log213��3.7bit
�@�ł���B
���̃J�[�h���n�[�g�̃L���O�ł��邱�Ƃ�m�������̏��ʂ͎��̂ǂꂩ�B
(1)�@1.2
(2)�@1.85
(3)�@3.1
(4)�@5.7
(5)�@7.4
�āF�S
A�J�[�h������̃}�[�N�ł���m����1/4�A����̐��ł���m����1/13�B
�v�͊m��C��log2C�Ƃ��ď���Ă���Ƃ������ƁB
�u�n�[�g�̃L���O�v�̂悤�ɓ���}�[�N�ŁA�����萔�ł���m����1/�i4*13�j��1/52�B
����āA���̏��ʂ́Alog252�B
22��4�A23��8�A24��16�A25��32�A26��64������A25��26�̊ԁB
����Đ�����5��6�̊ԁB
**********�F�l����̏��E���w�E*****������������ɏ������������܂����B���肪�Ƃ��������܂��B
log2(4*13)��log24�{log213��2�{3.7��5.7
**********
**********�F�l����̏��E���w�E*****aoki����ɏ������������܂����B���肪�Ƃ��������܂��B
�m���̖��ŁA�Z�I���[�ʂ�ł��B��͂�A�̒��O��ǂ݂܂��B
�u�n�[�g�̃L���O�v�F�ώ��ۂł��B
�o�i�`���a�j���o�i�`�j�~�o�i�a�j
�ɓ��Ă͂߂āA�������Q(4�~�P�R)�B
�g�P�S�̂P�������ł͓d�쎝�����݉\�ł����B�i�������ݕs�̋@�������܂����B�j�������Q(4�~�P�R)���v�Z�ł���d�쎝�����݂��\���g�P�T��������悭�ǂ݂܂��傤�B�w���A�ΐ��v�Z�̂ł���d��Ɋ���Ă����܂��傤�B
**********
���u2���Ƃ���ΐ��Ŋm��������Ă���v�Ƃ������[���ɋC�Â��Ίy���ł��B52��2�̉��悩���ׂ����o�����Ǝv��Ȃ����Ƃ���ł��B
�@���m�Ȑ��l�łȂ��A�u�ǂꂪ�������v���킩����� �Ƃ����̂�������̓����Ȃ̂ł�����B
��������������A�����ł���ˁB�` and B������P����A*B�ł�����ł���ˁB���̏ꍇ�ł��A�u13��2��3���4��̊ԁA4��ɋ߂��v�Ƃ��ĊT�Z���܂��B
�@�������A�������ĊF�l�ɂ��w�E�����������ƁA�u���w�I�ȓ��v�������Ă��邱�Ƃ�Ɋ����܂��B�Z�p�m�̒[����Ƃ��Ă͒p���ׂ����Ƃł��ˁB
��aoki����A�d�쎝�����߂���ł��ˁB���w�E�̒ʂ�A�w���E�ΐ��v�Z�Ȃǂ�d��Ńp�p�b�Ƃł��邱�Ƃ��K�v�Ȏ����ł��ˁB
(1)�@�C���^�[�l�b�g�̓R���s���[�^���m���ڑ����ꂽ���[�J���E�G���A�E�l�b�g���[�N�i�k�`�m�j�����݂ɐڑ�����Đ��E���ɍL�������l�b�g���[�N�ł���B
(2)�@�C���^�[�l�b�g��̓d�q���[���ł́A������摜�̃f�[�^���o�C�i���f�[�^�̌`�������̂܂ܑ��邱�Ƃ��ł���B
(3)�@�C���^�[�l�b�g��ɐڑ����ꂽ�R���s���[�^�ɂ́A1�䂲�Ƃɂh�o�A�h���X�ƌĂ�鎯�ʖ������Ă���B
(4)�@�C���^�[�l�b�g��̓d�q���[���́A�e�L�X�g�f�[�^�`���i7�r�b�g���������n�j�ł������𑗂�Ȃ��B
(5)�@�C���^�[�l�b�g�̕��y�́A������ɂ��e����^���Ă���B
�āF�Q
(2)��(4)���������邱�Ƃ������Ă���̂ŁA�ǂ��炩�������ł��邱�Ƃ��܂��킩��B����āA���̑��̑I�����͓ǂޕK�v�Ȃ��B
���[���ł͉摜�E�����Ȃǂ̃o�C�i���f�[�^���Y�t�t�@�C���Ƃ��đ����B
����������́A�G���R�[�h/�f�R�[�h�Ƃ����ϊ������������I�ɂ���Ă���̂ł��������邾���ŁA���ۂɂ͂��ׂẴf�[�^��7�r�b�gASCII�R�[�h�i�����f�[�^�j�ő����Ă���B���̃G���R�[�h/�f�R�[�h�@�\�𗘗p����7�r�b�g�����f�[�^�ȊO�̂��܂��܂ȃf�[�^�i�o�C�i���f�[�^�j�����[���ő���K�i���l�h�l�d�K�i�ŁAOutlookExpress��NetscapeMessenger�APostPet�Ȃǂ̎�v���[���[�͂���ɏ������Ă���B���ꂪ�u�Y�t�t�@�C���v�@�\�̐��̂ł���B
�y�Q�l�F�������z
8�r�b�g�����f�[�^�i�V�t�gJIS�Ȃǁj��ISO-2022-JP�Ƃ����R�[�h�̌n�ɕϊ�����7�r�b�g�����f�[�^�ő��M���Ă���B
�y�Q�l�F�������z
�ȏ�ɂ��A(4)�̋L�q�͐������A(2)�̋L�q�͌��ł���B
�������Y������͂��߂��낢��ȕ��ɏ������������܂����B�Ō�́u��͂�l�܂����ɂ��Ă��Ă͂����Ȃ��v�Ǝv���A�����Ȃ�ɒ��ׂČ��_���o���܂����B���͒P���ɓY�t�t�@�C���̓o�C�i���f�[�^�����̂܂ܑ����Ă���Ǝv���Ă��܂����B�p�\�R���ʐM����Ɂuish�v�Ƃ����ϊ��\�t�g�Ńe�L�X�g�f�[�^�ɒ����Ă��瑗�����肵�Ă����L���Łu�����ϊ��v�ȂǍl���Ȃ�������ł��ˁB����ish�������G���R�[�_/�f�R�[�_�������Ƃ́E�E�E�E�B�ł��A�������ɂȂ�܂����B
�����̑Ó������c�_�ɂȂ��Ă��܂������A�v���Ă��������P���ȓ����ł����B�u�Ƃɂ���E���[���Ƃ����̂�7�r�b�g�����f�[�^��������Ȃ��B�o�C�i���f�[�^���V�t�gJIS�������ϊ����đ����Ă�B�v�Ƃ������ƂŁA���ꂼ��K�i���������Ƃ������Ƃ�������ł��ˁB�u���쐬�҂��m���s���������̂ł́H�v�Ƌ^�������ƁA�쐬�҂ɂ��l�т������Ǝv���܂��B
�@
| �}1�D�����̉����Z�����`����\���} | �}2�D���C���̕�������`����\���} |
|
|
|
���̕�����̂����A�}2�̍\���}�ł͒�`����Ă��Ȃ����̂�I�ׁB
(1)�@��
(2)�@��
(3)�@����
(4)�@����
(5)�@������
�āF�S
�}2�̍\���}�Œ�`����Ȃ����̂�����A�}1�₻�̉�����͓ǂޕK�v�Ȃ��B
�}2���ƍl����A�܂����Ɋ�蓹����ꍇ������A���̏ꍇ�͂��Ɋ�蓹��������_���O�ɖ߂�B�����牽�x�����ɍs�����Ƃ����蓾��B
���̌�A���ɍs�������ɍs�����̑I��������A�����ʉ߂�����ŃS�[���B
���������āA���͉��x���ʂ蓾�邪�A����1���B�܂����̌�ɂ��ɍs�����Ƃ͂��蓾�Ȃ��B�����(4)�͂��蓾�Ȃ��B
�����ۓI�Ȑ}�ɔY�ނƃ_���ł��B�����Ȃǂ킩��₷�����̂ɗႦ�邱�Ƃ��|�C���g�B�܂��A�}1�₻�̉���������������������悤�Ƃ��Ȃ����Ƃ���ł��B