| (1) A | 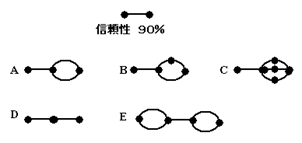 |
| (2) B | |
| (3) C | |
| (4) D | |
| (5) E |
| (事例№1) | ~わざわざ全部計算しなくてもいい例~ | 平成13年度一次試験基礎科目問題1 | 最終更新:2007.02.12 |
●問題文
次の図に示されるシステムの設計を考える。各システムは、節点を連結する線要素から構成されており、節点から節点に進むことのできる可能性(要素の信頼性)は90%である。ここで、それぞれのシステムを用いて左端から右端の節点に進むことのできる可能性、すなわち、システム全体の信頼性が最も高いのはどれか。
| (1) A |  |
| (2) B | |
| (3) C | |
| (4) D | |
| (5) E |
●解説
このような「どれが一番大きいか」的な大小比較問題では、とにかく数値を出して、その数値で比較しようとする人が少なからずおられますが、全部計算してから「どの数値が一番大きいか」考えるというのが一番非効率的な解き方です。
大小がわかればいいのですから、それぞれの数値まで出す必要はないのです。こういう問題は、2者間の大小比較をできるだけ計算せずに繰り返すのが一番効率的です。
| (解答例) | |
| *まずAとDを比べてみる。どちらも1ステップ目は直列で同じ。違いは2ステップ目が直列か並列か。並列のほうが信頼性が高いので、A>D。 ここですでにDは正解ではあり得ないので、Dの信頼性を計算することは不要。 *AとBを比較する。違いは並列の中に直列が1つ入っているところと2つ入っているところ。直列は多くなるほど信頼性が低くなるので、A>B。 ここでBも正解ではあり得なくなったので、Bも計算しない。 *AとEを比較。違いは1ステップ目の前に1つ並列が入っているかどうか。たとえ信頼性の高い並列でも何もないより信頼性は下がるので、A>E。 ここでEも正解ではあり得なくなったので、Eも計算しない。 *AとCを比較。違いは並列が2列か3列かということと、それぞれの並列の中に直列が1つ多く入っていること。 前者は信頼性アップに、後者は信頼性ダウンにつながる。つまり、これは計算しないと大小比較ができない。 *そこで計算するが、1ステップ目の直列はどちらも同じだから、計算する必要はない。並列部分だけ計算すればよい。 Aは1-{(1-0.9)×(1-0.9)}=0.99 Bは並列の各経路が直列2つなので0.9×0.9=0.81。これが3つ並列だから、1-{(1-0.81)×(1-0.81)×(1-0.81)}=0.993。 よって、A(0.99)<C(0.993) *ここで、1-0.81は0.19だが、これを「だいたい0.2」とすれば、1-0.23となるので、1-0.008=0.992となって、暗算でも答えは出る。 ここまでする必要はないでしょうが・・・・ |
|
このように、計算なしに二者択一まで進めます(仮にここで時間切れになったとしてもA・Cどちらかをあてずっぽうで書けば50%の確率で正解です)。そして計算は最後の1回ですみます。